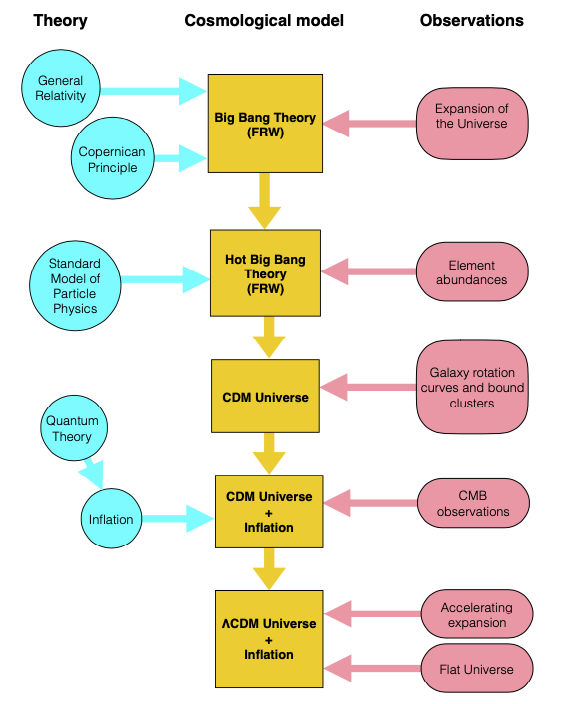
7 Philosophy of physics
What are good theories of the world?
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
7.1 Theories of matter
7.1.1 Ancient atomism
- Kanada (c. 700-100 BCE)
- Empedocles (c. 494-434 BCE)
- theory of the four elements
- Leucippus (fl. 5th century BCE)
- Democritus (c. 460-370 BCE)
- Epicurus (341-270 BCE)
- Lucretius (c. 99-55 BCE)
- De Rerum Natura translated by Esolen 1
1 Lucretius (1995), p. TODO.
Discussion:
- Weinberg
- Nail
- Nail claims that Lecretius was not an atomist, and that translations of Lecretius are colored by readings of his teacher, Epicurus. 2
- Crespo, H. (2018). Intro to book review of ontology of motion: On the subject of definitions.
2 Nail (2018).
7.1.2 Modern atomism
- Corpuscularianism
- Isaac Beeckman (1588-1637)
- René Descartes (1596-1650)
- Robert Boyle (1627-1691)
- John Locke (1632-1704)
- Isaac Newton (1642-1727)
- Yock, P. (2018). Newton’s hypotheses on the structure of matter. 3
- Henry Cavendish (1731-1810)
- Antoine Lavoisier (1743-1794)
- John Dalton (1766-1844)
- Law of multiple proportions (1803)
- Ludwig Boltzmann (1844-1906)
- Johannes Diderik van der Waals (1837-1923)
- Modern Atomism
- J.J. Thomson (1856-1940)
- Max Planck (1858-1947)
- Ernest Rutherford (1871-1937)
- Brownian motion
Discussion:
7.1.3 Contemporary views of matter
- Quantum field theory
- Statistical mechanics and condensed matter physics
- TODO: Brief nod to upcoming sections.
See also:
7.2 Classical physics
7.2.1 Mechanics
History:
- Isaac Newton (1642-1727)
- Gottfried Wilhelm Leibniz (1646-1716)
- Edmond Halley (1656-1742)
- Émilie du Châtelet (1706-1749)
- Conservation of energy in addition to conservation of momentum
- Leonhard Euler (1707-1783)
- Joseph-Louis Lagrange (1736-1813)
- Pierre-Simon Laplace (1749-1827)
- Carl Friedrich Gauss (1777-1855)
- Joseph von Fraunhofer (1787-1826)
- Augustin-Louis Cauchy (1789-1857)
- William Rowan Hamilton (1805-1865)
- Emmy Noether (1882-1935)
Lagrangian mechanics:
- TODO: explain
- Complaint about explanations of the Lagrangian:
Howe, A.R. (2020). Why does the Lagrangian equal T-V? - Relationship to the path-intergral formulation of quantum mechanics.
Pedagogy:
- The Feynman Lectures on Physics 9
- Holm’s Geometric Mechanics 10
- ’t Hooft, G. How to become a GOOD Theoretical Physicist.
Dimensional analysis:
- Tao, T. (2012). A mathematical formalisation of dimensional analysis.
- Buckingham \(\pi\) theorem 11
- physics.stackexchange.com: On the dot product of vectors in different vector spaces.
- Kasprzak, W., Lysik, B., & Rybaczuk, M. (1990). Dimensional Analysis in the Identification of Mathematical Models. 12
- Duff, M.J., Okun, L.B., & Veneziano, G. (2001). Trialogue on the number of fundamental constants. 13
- Janyska, J., Modugno, M., & Vitolo, R. (2007). Semi-vector spaces and units of measurement. 14
- Zapata-Carratala, C. (2021). Dimensioned algebra: The mathematics of physical quantities. 15
- TODO: Dimensional analysis can be formalized with each type of physical dimension having a corresponding vector space in a trivial vector bundle over a spacetime manifold, \(M\). Because the bundle projection, \(\pi\), is trivial, \(\pi: M \times \mathbb{R}^{n_1} \times \mathbb{R}^{n_2} \times \cdots \rightarrow M\), vectors in each vector space can be directly compared.
11 Buckingham (1914).
12 Kasprzak, Lysik, & Rybaczuk (1990).
13 Duff, Okun, & Veneziano (2001).
14 Janyska, Modugno, & Vitolo (2007).
15 Zapata-Carratala (2021).
See also:
7.2.2 Electrodynamics
History:
- Michael Faraday (1791-1867)
- Invented the concept of a field
- James Clerk Maxwell (1831-1879)
- Josiah Willard Gibbs (1839-1903)
- Oliver Heaviside (1850-1925)
Heaviside:
What is Maxwell’s theory? or, What should we agree to understand by Maxwell’s theory?
The first approximation to the answer is to say, There is Maxwell’s book as he wrote it; there is his text, and there are his equations: together they make his theory. But when we come to examine it closely, we find that this answer is unsatisfactory. To begin with, it is sufficient to refer to papers by physicists, written say during the twelve years following the first publication of Maxwell’s treatise, to see that there may be much difference of opinion as to what his theory is. It may be, and has been, differently interpreted by different men, which is a sign that it is not set forth in a perfectly clear and unmistakeable form. There are many obscurities and some inconsistencies. Speaking for myself, it was only by changing its form of presentation that I was able to see it clearly, and so as to avoid the inconsistencies. Now there is no finality in a growing science. It is, therefore, impossible to adhere strictly to Maxwell’s theory as he gave it to the world, if only on account of its inconvenient form. But it is clearly not admissible to make arbitrary changes in it and still call it his. He might have repudiated them utterly. But if we have good reason to believe that the theory as stated in his treatise does require modification to make it self-consistent, and to believe that he would have admitted the necessity of the change when pointed out to him, then I think the resulting modified theory may well be called Maxwell’s. 16
16 Heaviside (1893), pp. vi–vii.
Pedagogy:
- TODO
7.2.3 Special relativity
History:
- Ernst Mach (1838-1916)
- Mach’s principle
- Hendrik Lorentz (1853-1928)
- Henri Poincaré (1854-1912)
- Hermann Minkowski (1864-1909)
- Albert Einstein (1879-1955)
Stein:
And this is the crucial difference, as I see it, between Poincaré’s relation to the special theory of relativity and Einstein’s. Both of them discovered this theory—and did so independently. So far as its mathematical structure is concerned, Poincaré’s grasp of the theory was in some important respects superior to Einstein’s. But Einstein “took the theory seriously” in the sense that he looked to it for NEW INFORMATION about the physical world—that is, in Poincaré’s language, he regarded it as “fertile”: as a source of new “real generalizations”—of empirically testable consequences. And in doing so, Einstein attributed physical significance to the basic notions of the theory itself in a way that Poincaré did not. 19
19 Stein (2021), p. 69.
Pedagogy:
- Carnap, R. (1966). Philosophical Foundations of Physics. 20
- Maudlin 21
- Schroeder, D.V. (2022). Relativity in five lessons.
See also:
7.3 Statistical physics
7.3.1 Introduction
TODO:
- The goal of statistical mechanics.
- How statistical mechanics can be seen as pure mathematics.
- Statistical mechanics and thermodynamics
- Entropy
7.3.2 History
- James Clerk Maxwell (1831-1879)
- Josiah Willard Gibbs (1839-1903)
- Ludwig Boltzmann (1844-1906)
7.3.3 Thermodynamics
- Denker, J. (2021). Modern Thermodynamics.
- The 2nd Law of Thermodynamics said simply: Things tend to happen in ways for which there are many ways to happen like that.
7.3.4 Canonical ensemble
- Canonical ensemble
7.3.5 Phase translations
- Phase transitions
- Renormalization
- Universality
22 J. Wu (2021).
See also:
7.4 Symmetry-first physics
7.4.1 Curie’s principle
- Pierre Curie (1859-1906)
- Curie, P. (1894). On the symmetries of physical phenomenae, the electric field, and the magnetic field. (in French)
- “The symmetries of the causes are to be found in the effects.”
- Counting degrees of freedom
- Totalitarian principle: “Everything not forbidden is compulsory.” - Murray Gell-Mann
- Caulton, A. (2015). The role of symmetry in the interpretation of physical theories. 23
- Caulton, A. & Butterfield, J. (2012). Symmetries and paraparticles as a motivation for structuralism. 24
- de Queiroz, A., Lachieze-Rey, M., & Simon, S. (2014). Symmetry, physical theories and theory change. 25
See also:
7.4.2 Relativity
- Special relativity
- Leibniz-Clarke correspondence
- Einstein (1905)
- Lorentz group
- Minkowski spacetime
See also:
7.4.3 Noether’s theorems
- Principle of least action, Lagrangians
- Canonical dynamics
- Noether, E. (1918). Invariante variationsprobleme. 26
- TODO: Noether’s first and second theorem.
- Wigner, E.P. (1954). Conservation laws in classical and quantum physics. 27
- Brading, K.A. (2002). Which symmetry? Noether, Weyl, and conservation of electric charge. 28
- Baez, J.C. (2018). Getting to the bottom of Noether’s theorem. Talk given at The Philosophy and Physics of Noether’s Theorems. 29
- Goyal, P. (2020). Derivation of classical mechanics in an energetic framework via conservation and relativity. 30
7.4.4 Gauge principle
- Weyl, H. (1918). Raum, Zeit, Materie. 31
- Weyl, H. (1929). Elektron und gravitation. 32
- Pauli, W. (1941). Relativistic field theories of elementary particles. 33
- Yang C.N. & Mills R.L. (1954). Conservation of isotopic spin and isotopic gauge invariance. 34
- ’t Hooft, G. (1994). Under the Spell of the Gauge Principle. 35
- Yang, C.N. (1996). Symmetry and physics. 36
- O’Raifeartaigh, L. (1997). The Dawning of Gauge Theory. 37
- Teller, P. (2000). The gauge argument. 38
- ’t Hooft, G. (2007). Lie groups in physics. 39
- Greaves, H. & Wallace, D. (2011). Empirical consequences of symmetries. 40
- Afriat, A. (2013). Weyl’s gauge argument. 41
- Schwichtenberg, J. (2015). Physics from Symmetry. 42
- Dewar, N. (2019). Sophistication about symmetries. 43
31 Weyl (1918).
32 Weyl (1929).
33 Pauli (1941).
34 Yang & Mills (1954).
35 ’t Hooft (1994).
36 Yang (1996).
37 O’Raifeartaigh (1997).
38 Teller (2000).
39 ’t Hooft (2007).
40 Greaves & Wallace (2011).
41 Afriat (2013).
42 Schwichtenberg (2015).
43 Dewar (2019).
Weyl:
It seems to me that this new principle of gauge invariance, which follows not from speculation but from experiment, compellingly indicates that the electromagnetic field is a necessary accompanying phenomenon, not of gravitation, but of the material wave field represented by \(\psi\). Since gauge invariance includes an arbitrary function \(\lambda\) it has the character of “general” relativity and can naturally only be understood in that context. 44
44 Weyl (1929), p. TODO.
7.4.5 Wigner-Stone theorems
- Stone’s theorem on one-parameter unitary groups (1930, 1932)
- For any strongly continuous one-parameter unitary group, \(U(t)\), \(\exists \: A = A^\dagger \: | \: U(t) = e^{i\,t\,A} \ \forall \: t \in \mathbb{R}\).
- Stone–von Neumann theorem (1931, 1932)
- Establishes the uniqueness of the canonical commutation relations between position and momentum operators.
- Wigner’s theorem (1931)
- Wigner, E.P. (1959). Group Theory and its Application to the Quantum Mechanics of Atomic Spectra. 45
- The theorem specifies how physical symmetries such as rotations, translations, and CPT are represented on the Hilbert space of states.
- Kadison, R.V. (1965). Transformations of states in operator theory and dynamics. 46
Ovrut’s version of Wigner’s theorem:
The generators of the representation of a transformation in the Hilbert space are the operators representing the classical Noether’s charges that are conserved under that transformation. 47
47 Reece (2007), p. 27.
Discussion:
- Schweber, S.S. (1961). An Introduction to Relativistic Quantum Field Theory. 48
- Simon, B. (1976). Quantum dynamics: From automorphism to Hamiltonian. 49
- Summers, S.J. (1999). On the Stone-von Neumann uniqueness theorem and its ramifications. 50
- Keller, K.J., Papadopoulos, M.A., & Reyes-Lega, A.F. (2007). On the realization of symmetries in quantum mechanics. 51
- Schroeren, D. (2021). Symmetry fundamentalism in quantum mechanics. 52
- Wigner’s theorem - nLab
48 Schweber (1961), p. TODO.
49 B. Simon (1976).
50 Summers (1999).
51 Keller, Papadopoulos, & Reyes-Lega (2007).
52 Schroeren (2021).
See also:
7.5 Quantum mechanics
7.5.1 Introduction
- Hilbert spaces; Wigner’s theorem; Born rule
- Wave-particle duality misconceptions. Fields are more fundamental than particles.
- Philosophy of QM traditionally focus on NRQM. 53
- The measurement problem. Decoherence. The Born rule again.
- Uncertainty principle
- Relationship to the Gabor limit
- Decoherence brings quantum logic to classical logic?
53 Ney & Albert (2013).
Feynman and Hibbs on wave-principle duality:
What is remarkable is that this dual use of wave and particle ideas does not lead to contradictions. This is so only if great care is taken as to what kind of statements one is permitted to make about the experimental situation. 54
54 Feynman & Hibbs (1965), p. 6.
Feynman and Hibbs on the uncertainty principle:
7.5.2 History
- History of quantum mechanics
- Kelvin, L. (1901). Nineteenth century clouds over the dynamical theory of heat and light. 56
- Hendrik Lorentz (1853-1928)
- Max Planck (1858-1947)
- Marie Curie (1867-1934)
- Albert Einstein (1879-1955)
- Max Born (1882-1970)
- Niels Bohr (1885-1962)
- Arnold Sommerfeld (1868-1951)
- Erwin Schrödinger (1887-1961)
- Louis de Broglie (1892-1987)
- Lawrence Bragg (1890-1971)
- Wolfgang Pauli (1900-1958)
- Werner Heisenberg (1901-1976)
- Paul Dirac (1902-1984)
- An introduction to the Solvay conferences on physics - Université PSL
- Bacciagaluppi, G. & Valentini, A. (2009). Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference. 57
- Proceedings of the Solvay conferences on physics

- Pascual Jordan (1902-1980)
- Eugene Wigner (1902-1995)
- John von Neumann (1903-1957)
- J. Robert Oppenheimer (1904-1967)
- John Archibald Wheeler (1911-2008)
- Richard P. Feynman (1918-1988)
- Freakonomics 3-part radio series about Feynman: The Curious, Brilliant, Vanishing Mr. Feynman
7.5.3 Hydrogen atom
- Factorizable in spherical coordinates, leading to solutions as a product of spherical harmonics in (\(\theta\), \(\phi\)) and Laguerre polynomials in \(r\).
- Fine structure
- Lamb shift
- Hyperfine structure
7.5.4 Foundations of QM
7.5.4.1 Hilbert spaces
States being represented as vectors in a Hilbert space implies the superposition principle:
\[ |\psi\rangle = \sum_{n} a_{n} \: |n\rangle \]
the definition of a complex inner product:
\[ \langle\psi_1|\psi_2\rangle = \int dx \: \langle\psi_1|x\rangle \, \langle{}x|\psi_2\rangle \]
and a norm:
\[ \langle\psi|\psi\rangle \geq 0 \]
7.5.4.2 Operators
Observables are represented as self-adjoint operators with the “eigenvector-eigenvalue link.”
\[ \hat{H} \: |n\rangle = E_{n} \: |n\rangle \]
7.5.4.3 Wigner’s theorem
The generators of the representation of a transformation in a Hilbert space are the operators representing the classical Noether charges that are conserved under that transformation.
\[ \hat{U}(x^{\mu}) = \exp( -i \, x^\mu \, \hat{P}_\mu ) \]
\[ \hat{U}(\theta^{\mu\nu}) = \exp( \frac{-i}{2} \, \theta^{\mu\nu} \, \hat{M}_{\mu\nu} ) \]
7.5.4.4 Born rule
\[ P(n) = | \langle n | \psi \rangle |^{2} = |a_{n}|^{2} \]
TODO: Note that Everettian QM would argue the Born rule is secondary and derivable.
7.5.4.5 Discussion
- Orthodox QM
- Moretti, V. (2015). Mathematical foundations of quantum mechanics: An advanced short course. 60
- Wallace, D. (2016). What is orthodox quantum mechanics? 61
- Carcassi, G., Maccone, L., & Aidala, C.A. (2020). The four postulates of quantum mechanics are three. 62
- Too much focus on NRQM
- Wallace, D. (2020). Lessons from realistic physics for the metaphysics of quantum theory. 63
- Somehow, QM is about complex numbers:
- Riesz representation theorem
- Jordan, P., von Neumann, J., & Wigner, E.P. (1934). On an algebraic generalization of the quantum mechanical formalism. 64
- Baez, J.C. (2011). Division algebras and quantum theory. 65
- Morales, J.A.C & Zilber. B. (2014). The geometric semantics of algebraic quantum mechanics. 66
- Garisto, D. (2025). Physicists take the imaginary numbers out of quantum mechanics.
- TODO: References therein
- Hilbert spaces
- Rédei, M. (1996). Why John von Neumann did not like the Hilbert space formalism of quantum mechanics (and what he liked instead). 67
- de la Madrid, R. (2005). The role of the rigged Hilbert space in quantum mechanics. 68
- Carcassi, G., Calderon, F., & Aidala, C.A. (2023). The unphysicality of Hilbert spaces. 69
- Kronz, F. & Lupher, T. (2024). Quantum theory and mathematical rigor. - SEP
- Erdős-Kaplansky theorem
60 Moretti (2015).
61 Wallace (2016).
62 Carcassi, Maccone, & Aidala (2020).
63 Wallace (2020).
64 Jordan, Neumann, & Wigner (1934).
65 Baez (2011).
66 Morales & Zilber (2014).
67 Rédei (1996).
68 de la Madrid (2005).
69 Carcassi, Calderon, & Aidala (2023).
See also:
7.5.5 Secondary properties of QM
- Wave function:
\[ \langle x | n \rangle = \psi_{n}(x) \]
- Schrödinger equation:
\[ i \hbar \: \partial_{t} \: |\psi\rangle = \hat{H} \: |\psi\rangle \]
- Heisenberg picture:
\[ i \hbar \: \partial_{t} \: \hat{U}(t) \: |\psi\rangle = \hat{H} \: \hat{U}(t) \: |\psi\rangle \]
Schrödinger vs Heisenberg pictures is like Heraclitus vs Parmenides.
Heisenberg uncertainty principle - Derivable from the Gabor limit in time-frequency analysis
Decoherence
\[ \mathcal{H} = \mathcal{H}_\mathrm{S} \otimes \mathcal{H}_\mathrm{E} \]
\[ |\psi\rangle \otimes |\alpha\rangle \rightarrow |\psi; \alpha\rangle \otimes |\alpha\rangle \]
See Dutailly 70, for example, for a demonstration that the Schrödinger equation is derivable from Wigner’s theorem.
70 Dutailly (2014), p. 11–13.
7.5.6 Decoherence
- Schrödinger, E. (1952). Are there quantum jumps? Part I. 71
- Schrödinger, E. (1952). Are there quantum jumps? Part II. 72
- Born, M. (1953). The interpretation of quantum mechanics. 73
- Joos, E. & Zeh, H. D. (1985). The emergence of classical properties through interaction with the environment. 74
- Bell, J.S. (1987). Are there quantum jumps? 75
- Zurek, W.H. (1991). Decoherence and the transition from quantum to classical. 76
- Zurek, W.H. (2001). Decoherence, einselection, and the quantum origins of the classical. 77
- Zurek, W.H. (2003). Decoherence and the transition from quantum to classical–Revisited. 78
- Decoherence and the Appearance of a Classical World in Quantum Theory 79
- Leggett, A.J. (2002). Testing the limits of quantum mechanics: Motivation, state of play, prospects. 80
- Schlosshauer, M. (2005). Decoherence, the measurement problem, and interpretations of quantum mechanics. 81
- My quora answer: What is currently the best explanation for how and why the quantum wave function collapses?
- Decoherence and Everett’s interpretation
- Drossel, B. (2015). On the relation between the second law of thermodynamics and classical and quantum mechanics. 82
- Wallace, D. (2018). Decoherence and its role in the modern measurement problem. 83
- Zurek, W.H. (2022). Quantum theory of the classical: Einselection, envariance, quantum Darwinism and extantons. 84
- Natura non facit saltus
- Nagele, C., Janssen, O., & Kleban, M. (2023). Decoherence: A numerical study. 85
71 Schrödinger (1952a).
72 Schrödinger (1952b).
73 Born (1953).
74 Joos & Zeh (1985).
75 Bell (2004a).
76 Zurek (1991).
77 Zurek (2001).
78 Zurek (2003).
79 Joos, E. et al. (2003).
80 Leggett (2002).
81 Schlosshauer (2005).
82 Drossel (2015), p. 51–2.
83 Wallace (2018).
84 Zurek (2022).
85 Nagele, Janssen, & Kleban (2023).
See also:
7.5.7 Quantum chemistry
- Cohen, M.L. (2015). Explaining and predicting the properties of materials using quantum theory. 86
- Friedrich, B. (2016). How did the tree of knowledge get its blossom? The rise of physical and theoretical chemistry, with an eye on Berlin and Leipzig. 87
- Density functional theory
- Cao, C., Hu, H., Li, J., & Schwarz, W.H.E. (2019). Physical origin of chemical periodicities in the system of elements. 88
- Seifert, V.A. (2024). The chemical bond is a real pattern. 89
7.5.8 Quantum computing
- Feynman
- Coecke, B. & Kissinger, A. (2017). Picturing Quantum Processes: A first course in quantum theory and diagrammatic reasoning. 90
- Preskill, J. (2018). Quantum computing in the NISQ era and beyond. 91
- Arute, F. et al. (2019). Quantum supremacy using a programmable superconducting processor. 92
- Google AI Blog. (2019). Quantum supremacy using a programmable superconducting processor.
- Broughton, M. et al. (2020). TensorFlow Quantum: A software framework for quantum machine learning. 93
- TensorFlow. (2020). tensorflow.org/quantum.
- TensorFlow. (2021). Quantum machine learning concepts.
- Preskill, J. (2021). Quantum computing 40 years later. 94
7.6 Quantum field theory
7.6.1 Fields
7.6.1.1 Introduction
- Field concept/definition: Laplace, Faraday
- Richard Feynman (1918-1988)
- Julian Schwinger (1918-1994)
- Shin’ichirō Tomonaga (1906-1979)
- Feynman’s Nobel Lecture on QED 95
- Weinberg’s folk theorem: QFT is the right way to combine Lorentz invariance, quantum mechanics, and the cluster decomposition principle. 96
- Euler-Lagrange equations of motion
- The Dirac equation does not describe a relativistic wavefunction (hence the obsolete “Dirac sea” interpretation). 97
Baez, Segal, & Zhou:
Quantum field theory is quintessentially the algebra and analysis of infinite-dimensional dynamical systems, as constrained by quantum phenomenology, causality, and symmetry. Although it has a clear-cut central goal, that of the realistic description of particle production and annihilation in terms of the localized interactions of fields in space-time, it is clear from this description that it is a multifaceted subject. 98
98 Baez, Segal, & Zhou (1992), p. 1.
7.6.1.2 Pedagogy
- Peskin and Schroeder 99
- Weinberg, S. (1995). The Quantum Theory of Fields: Volume 1 Foundations. 100
- Zee 101
- Schwartz 102
- David Tong 103
- Zeidler, vol 1 104, 2 105, and 3 106
- Cao, T.Y. (1999). Conceptual Foundations of Quantum Field Theory. 107
- ’t Hooft, G. (2005). The conceptual basis of quantum field theory. 108
- Reece, R. (2007). Quantum field theory: An introduction. 109
- Mulders, P.J. (2011). Quantum field theory. 110
- Kocic, M. (2016). Handout: Overview of the fields in QFT.
7.6.2 Symmetry
7.6.2.1 Introduction
- TODO
- Noether’s theorem, again
- Wigner-Stone theorems, again
See also:
7.6.2.2 Coleman-Mandula theorem
- Coleman-Mandula theorem 111
111 Coleman & Mandula (1967).
See also:
7.6.2.3 Wigner’s classification
- Wigner’s classification (1939) 112
- Gross, D.J. (1996). The role of symmetry in fundamental physics. 113
7.6.2.4 CPT theorem
- Bell, J.S. (1955). Time reversal in field theory. 114
- Streater, R. & Wightman, A. (1964). PCT, spin and statistics, and all that. 115
- Greaves, H. & Thomas, T. (2012). The CPT theorem. 116
7.6.3 Spin
7.6.3.1 Introduction
7.6.3.2 Spinors
- Spinor
- SU(2) double covers SO(3)
- Belt trick
- Orientation entanglement
- Spatial vectors alone are not sufficient to describe fully the properties of rotations in space.
- Penrose, R. & Weinstein, E. (2020). Video: Do we understand spinors?
- In some sense, a spinor is the square-root of a vector.
Michael Atiyah:
No one fully understands spinors. Their algebra is formally understood but their general significance is mysterious. In some sense they describe the “square root” of geometry and, just as understanding the square root of -1 took centuries, the same might be true of spinors. 120
120 Dutailly (2014), p. 37.
7.6.3.3 Spin-statistics theorem
- Spin-statistics theorem - Pauli
7.6.4 Scattering
- Correlation AKA Green’s functions
- Feynman propagator
- Källén-Lehmann spectral representation
- Wick’s theorem
- Schlingemann, D. (1998). From euclidean field theory to quantum field theory. 121
- Kontsevich, M. & Segal, G. (2021). Wick rotation and the positivity of energy in quantum field theory. 122
- Gell-Mann and Low theorem
- Interaction picture
- Vaccuum bubble cancelation
- Gell-Mann, M. & Low, F. (1951). Bound states in quantum field theory. 123
- Molinari, L.G. (2006). Another proof of Gell-Mann and Low’s theorem. 124
- Dyson series
- Dyson, F.J. (1949). The \(S\) matrix in quantum electrodynamics. 125
- Dyson, F.J. (1952). Divergence of perturbation theory in quantum electrodynamics. 126
- Baez, J. (2016). Struggles with the continuum, part 6.
- LSZ reduction formula
- Lehmann, H., Symanzik, K., & Zimmermann, W. (1955). Zur formulierung quantisierter feldtheorien. 127
- Buchholz, D. & Dybalski, W. (2005). Scattering in relativistic quantum field theory: basic concepts, tools, and results. 128
- Feynman diagrams and Feynman rules
- Weinberg, S. (1964). Feynman rules for any spin. 129
- Pedagogy
- Martin, S.P. (2011). Phenomenology of particle physics. 130
- Martin, S.P. & Wells, J.D (2023). Elementary Particles and Their Interactions. 131
- Discussion
- Jaeger, G. (2019). Are virtual particles less real? 132
7.6.5 Path intergrals
- Feynman
- Feynman and Hibbs (1965) 133
- Partition functions and generating functionals
- Show this way of deriving the Feynman rules
- Nguyen, T. (2016). The perturbative approach to path integrals: A succinct mathematical treatment. 134
- Gill, T.L. (2017). The Feynman-Dyson view. 135
7.6.6 Renormalization
- Dyson
- Dirac, P.A.M. (1963). The evolution of the physicist’s picture of nature. 136
- ’t Hooft, G. (1971). Renormalizable Lagrangians for massive Yang-Mills fields. 137
- Wilson, K.G. (1974). The renormalization group and the \(\varepsilon\) expansion. 138
- Wilson, K.G. (1979). Problems in physics with many scales of length. 139
- Goldenfeld, N. (1992). Lectures on Phase Transitions and the Renormalization Group. 140
- ’t Hooft, G. (1994). Under the Spell of the Gauge Principle. (again) 141
- ’t Hooft, G. (1999). A confrontation with infinity (Nobel lecture). 142
- Borcherds, R.E. & Barnard, A. (2002). Lectures on quantum field theory. 143
- The “renormalization group” isn’t a group; it’s actually a semigroup. The reason that renormalization produces a semigroup is that a block transformation loses information. 144
- Butterfield, J. (2014). Reduction, emergence, and renormalization. 145
- Butterfield, J. & Bouatta, N. (2015). Renormalization for philosophers. 146
- Universality is multiple realizability
- Fraser, J.D. (2021). The twin origins of renormalization group concepts. 147
- Phillips, P.W. (2023). Fifty years of Wilsonian renormalization and counting. 148
- Video: Moving Naturalism Forward, Day 1, Afternoon, 2nd Session: Simon DeDeo on renormalization.
7.6.7 Effective field theory
- Effective field theory (EFT)
- Huggett, N., & Weingard, R. (1995). The renormalisation group and effective field theories. 149
- Weinberg, S. (1997). What is quantum field theory, and what did we think it is?. 150
- Cao, T.Y. (2003). Structural realism and the interpretation of quantum field theory. 151
- Bain, J. (2013). Effective field theories. 152
- Preskill, J. (2013). We are all Wilsonians now. 153
- Glick, D. (2016). The ontology of quantum field theory: Structural realism vindicated?. 154
- Williams, P. (2019). Scientific realism made effective. 155
- Ruetsche, L. (2018). Renormalization group realism: The ascent of pessimism. 156
- Fraser, J.D. (2018). Renormalization and the formulation of scientific realism. 157
- Halvorson, H. (2019). To be a realist about quantum theory. 158
- Rosaler, J. (2022). Dogmas of effective field theory: Scheme dependence, fundamental parameters, and the many faces of the Higgs naturalness principle. 159
149 Huggett & Weingard (1995).
150 Weinberg (1997b).
151 T. Y. Cao (2003).
153 Preskill (2013).
154 Glick (2016).
155 Williams (2019).
156 Ruetsche (2018).
157 J. D. Fraser (2018).
158 Halvorson (2019).
159 Rosaler (2022).
J.D. Fraser:
in demonstrating that these large scale properties of a QFT model are insensitive to what is going on at very high energies, the renormalization group is also telling us that these features are largely independent of the details of unknown physics at currently inaccessible energy scales. We thus have reason to be confident that these features of current QFTs will be retained through future theory change, in one way or another, whatever physics beyond the standard model has in store for us. 160
160 J. D. Fraser (2018), p. 10.
7.6.8 Foundations of QFT
7.6.8.1 Introduction
- Weinberg
- Reeh-Schlieder theorem
- Taj Mahal principle
- Struggles with the continuum 161
- Auyang, S.Y. (1995). How Is Quantum Field Theory Possible? 162
Baez:
Nobody has found a fully rigorous formulation of QED, nor has anyone proved such a thing cannot be found. 163
163 Baez (2016), p. 17.
Baez:
In practice, quantum field theory is marvelously good for calculating answers to many physics questions. The answers involve approximations. These approximations seem to work very well: that is, the answers match experiments. Unfortunately we do not fully understand, in a mathematically rigorous way, what these approximations are supposed to be approximating. 164
164 Baez (2016), p. 18.
7.6.8.2 Wave-particle duality
- Einstein, A. (1905). On a heuristic point of view about the creation and conversion of light. 165
- Schrödinger, E. (1953). What is matter?. 166
- Wolchover, N. (2020). What is a particle?
The so-called wave-particle paradox is similar to the paradox that arises from attributing life or death to the quantum cat. A system is often said to be a particle if a position eigenvalue is observed and a wave if a momentum eigenvalue is observed, hence it is said to present a paradox. The paradox is the result of fallacious attribution. Both eigenvalues are classical quantities, and neither can be attributed to the system as its property. The property of the quantum system is its wavefunction in the position representation and momentum amplitude in the momentum representation. Either one of them offers a complete description, and the descriptions can be shown to be equivalent by rigorous transformations. Paradox arises only when interpreters insist on considering exclusively classical quantities that we can observe. The insistency closes the mind to quantum properties. 167
167 Auyang (1995), p. 80.
Weinberg on wave-particle duality:
In its mature form, the idea of quantum field theory is that quantum fields are the basic ingredients of the universe, and particles are just bundles of energy and momentum of the fields. In a relativistic theory the wave function is a functional of these fields, not a function of particle coordinates. Quantum field theory hence led to a more unified view of nature than the old dualistic interpretation in terms of both fields and particles. 168
168 Weinberg (1997b), p. 2.
- Weinberg, S. (1997). What is an elementary particle? 169
169 Weinberg (1997a).
Baez, Segal, & Zhou on wave-particle duality:
The treatment of the dynamics of quantum systems turns out to be naturally undertaken in terms of field rather than particle concepts, by virtue of the local character of relativistic interactions. In mathematical terms, the field is diagonalized in the functional integration representation, just as the particle numbers are diagonalized in the tensor product representation. 170
170 Baez et al. (1992), p. 59.
- Albert: QFT can be shown to derive NRQM. 171
- Fraser, D. (2008). The fate of ‘particles’ in quantum field theories with interactions. 172
- Baker, D.J. (2009). Against field interpretations of quantum field theory. 173
- Pessa, E. (2009). The concept of particle in quantum field theory. 174
- Duncan, A. (2012). The Conceptual Framework of Quantum Field Theory. 175
- Lazarovici, D. (2018). Against fields. 176
7.6.8.3 Quantization
- Canonical quantization
- Path integral quantization
- No “2nd quantization”
- Geometric quantization
- Weyl
- Dirac quantization and magnetic monopoles
- Todorov, I. (2012). Quantization is a mystery. 179
- Schreiber, U. (2016). Higher prequantum geometry. 180
- Instead of quantizing classical theories, should we be finding the classical limit of quantum theories?
7.6.8.4 Newton-Wigner localization
TODO: Clean up
Single-particle states:
\[ | \vec{x}, t \rangle = \hat{\psi}(\vec{x}, t) | 0 \rangle \]
and single-particle wavefunction derived from QFT: 181
181 Myrvold (2015), p. 15.
\[ \psi(x) = \langle x | \Psi \rangle = \langle 0 | \hat{\psi}(x) | \Psi \rangle \]
- Newton-Wigner localization
- Newton, T.D. & Wigner, E.P. (1949). Localized states for elementary systems. 182
- Fleming, G.N. (2000). Reeh-Schlieder meets Newton-Wigner. 183
- Myrvold, W.C. (2015). What is a wavefunction? 184
- Moretti, V. (2023). On the relativistic spatial localization for massive real scalar Klein-Gordon quantum particles. 185
7.6.8.5 Haag’s theorem
- Haag’s theorem
- Haag, R. (1955). On quantum field theories. 186
- The interaction picture does not exist in interacting relativistic QFT.
- States in the free theory are unitarily inequivalent to those in interacting relativistic QFT.
- \(O_\mathrm{int} \neq U \: O_\mathrm{free} \: U^{-1}\)
- Discussion:
- Malament, D.B. (1996). In defence of dogma: Why there cannot be a relativistic quantum mechanics of (localizable) particles. 187
- Teller, P. (1997). An Interpretive Introduction to Quantum Field Theory. 188
- Earman, J. & Fraser, D. (2006). Haag’s theorem and its implications for the foundations of quantum field theory. 189
- Klaczynski, L. (2016). Haag’s theorem in renormalised quantum field theories. 190
- Ruetsche, L. (2002). Interpreting quantum field theory. 191
- Resolution:
- Bain, J. (2000). Against particle/field duality: Asymptotic particle states and interpolating fields in interacting QFT, or Who’s afraid of Haag’s theorem? 192
- FAPP-localized particles
- Duncan, A. (2012). Conceptual Framework of Quantum Field Theory. 193
- TODO: Wallace
- QFT requires an ultraviolet regulator (a cutoff, a lattice), and Haag’s theorem does not apply when the regulator is in place.
- Seidewitz, E. (2017). Avoiding Haag’s theorem with parameterized quantum field theory. 194
- TODO: Is the resolution of Haag’s theorem related to separable (but infinite dimensional) Hilbert spaces?
- Bain, J. (2000). Against particle/field duality: Asymptotic particle states and interpolating fields in interacting QFT, or Who’s afraid of Haag’s theorem? 192
186 Haag (1955).
187 Malament (1996).
188 Teller (1997), p. 115.
189 Earman & Fraser (2006).
190 Klaczynski (2016).
191 Ruetsche (2002).
192 Bain (2000).
193 Duncan (2012), p. 359.
194 Seidewitz (2017).
I have really fallen into a rabbit hole over Haag's theorem. #HaagsTheorem #philsci #philqft pic.twitter.com/6DhBpnWPKQ
— Ryan Reece (&commm;RyanDavidReece) September 13, 2017
You all weren't much help on Haag's theorem.
— Ryan Reece (&commm;RyanDavidReece) September 21, 2017
Duncan, A. (2012). Conceptual Framework of QFT. Oxford. p. 359. pic.twitter.com/NIHgfNh7s6
7.6.8.6 Bootstrap theory
7.6.8.7 Causal perturbation theory
nLab (Schreiber):
Causal perturbation theory may be regarded as providing a well-defined consistent generalization from quantum mechanics to quantum field theory on Lorentzian spacetimes of the construction of the \(S\)-matrix via the Dyson formula (“time-ordered products”) in the interaction picture. 197
197 nLab authors (2021a).
First rigorous perturbation theory in QFT according to Schreiber:
- Epstein, H. & Glaser, V. (1973). The role of locality in perturbation theory. 198
198 Epstein & Glaser (1973).
7.6.8.8 Algebraic vs constructive QFT
- AQFT vs LQFT
- Haag-Ruelle scattering theory
- Haag, R. (1992). Local Quantum Physics: Fields, Particles, Algebras. 199
- Buchholz, D. (1998). Current trends in axiomatic quantum field theory. 200
- Wallace, D. (2011). Taking particle physics seriously: A critique of the algebraic approach to quantum field theory. 201
- Fraser, D. (2011). How to take particle physics seriously: A further defence of axiomatic quantum field theory. 202
Kastler:
Rudolf [Haag] is not satisfied by a notion of local observables relying plainly on space and time. Instead he wishes to base the theory on concepts related to individual processes. This attitude seems to me to move towards a basic “algebra of procedures”, pointing towards a theory of (non-commutative) space-time. I know that, coming from a very different angle, Alain Connes also believes the ultimate algebra of basic physics to be a discrete algebra of elements standing for experimental procedures—following the idea that the spatial notions man acquires in his cradle are less basic than his procedures at [particle] accelerators. 203
203 Kastler (2003), p. 6.
7.7 Exotics in quantum field theory
7.7.1 Gauge theory
7.7.1.1 Aharonov-Bohm effect
- Aharonov, Y. & Bohm, D. (1959). Significance of electromagnetic potentials in quantum theory. 204
- Maudlin, T. (1998). Healey on the Aharonov-Bohm effect. 205
- Healey, R. (2007). Gauging What’s Real. 206
- Batterman, R. (2003). Falling cats, parallel parking and polarized light. 207
- Holonomy
- Wallace, D. (2014). Deflating the Aharonov-Bohm effect. 208
- Maudlin, T. (2018). Ontological clarity via canonical presentation: Electromagnetism and the Aharonov-Bohm effect. 209
204 Aharonov & Bohm (1959).
205 Maudlin (1998).
206 Healey (2007), ch. 2-4.
207 Batterman (2003).
208 Wallace (2014).
209 Maudlin (2018).
Wikipedia discussion in the magnetic moment article:
A gauge theory like electromagnetism is defined by a gauge field, which associates a group element to each path in space time. For infinitesimal paths, the group element is close to the identity, while for longer paths the group element is the successive product of the infinitesimal group elements along the way.
In electrodynamics, the group is \(U(1)\), unit complex numbers under multiplication. For infinitesimal paths, the group element is \(1 + i\,A_\mu\,dx^\mu\) which implies that for finite paths parametrized by \(s\), the group element is:
\(\prod _{s}\left(1+i\,e\,A_\mu\,\frac{dx^\mu}{ds}\,ds\right) = \exp\left(i\,e\int A\cdot dx\right) \,.\)
The map from paths to group elements is called the Wilson loop or the holonomy, and for a \(U(1)\) gauge group it is the phase factor which the wavefunction of a charged particle acquires as it traverses the path. For a loop:
\(e\oint_{\partial D}A\cdot dx = e\int_{D}(\nabla \times A)\,dS = e\int_{D}B\,dS \,.\)
So that the phase a charged particle gets when going in a loop is the magnetic flux through the loop. When a small solenoid has a magnetic flux, there are interference fringes for charged particles which go around the solenoid, or around different sides of the solenoid, which reveal its presence.
7.7.1.2 Fiber bundles
A fiber bundle is locally a product space, \(X \times G\), of a base space, \(X\), and a fiber space, \(G\). In general, fiber bundles may have non-trivial global structure (e.g. a Mobius strip), but commonly in the ordinary use in physics, trivial bundles are used where the fiber bundle is just \(X \times G\) globally. The base space is spacetime, and the fiber is the space of possible gauge transformations.
- Fiber bundle
- Fiber bundles in physics - nLab
- Fiber bundles embody two central principles of modern physics:
- the principle of locality
- the gauge principle.
- In Yang-Mills theories, the gauge fields are not just local differential 1-forms, \(A_{\mu}\), but are globally really connections on principle bundles, and this is all-important once one passes to non-perturbative Yang-Mills theory, hence to the full story, instead of its infinitesimal or local approximation.
- Fiber bundles embody two central principles of modern physics:
- Wu, T.T. & Yang, C.N. (1975). Concept of nonintegrable phase factors and global formulation of gauge fields. 210
210 T. T. Wu & Yang (1975).
Bundles are the global structure of physical fields and they are irrelevant only for the crude local and perturbative description of reality. 211
211 nLab authors (2021b).
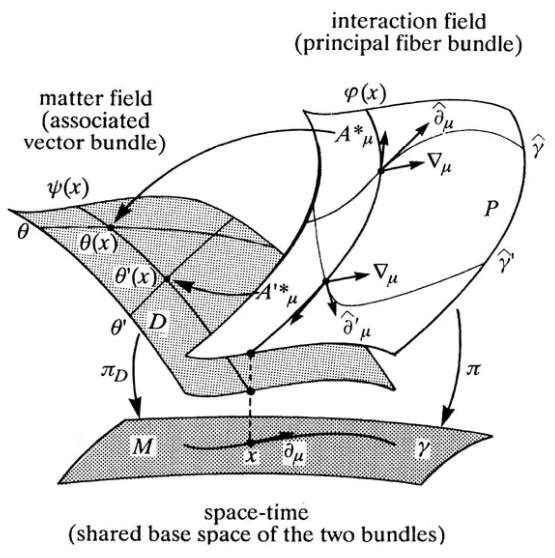
212 Auyang (1995), p. 220.
- Auyang, S.Y. (1995). How Is Quantum Field Theory Possible? 213
- Auyang, S.Y. (2000). Mathematics and reality: Two notions of spacetime in the analytic and constructionist views of gauge field theories. 214
- Frankel, T. (2004). The Geometry of Physics. 215
- Way, R. (2010). Introduction to connections on principal fibre bundles. 216
- Vákár, M. (2011). Principal bundles and gauge theories. 217
- Marsh, A. (2016). Gauge theories and fiber bundles: Definitions, pictures, and results. 218
213 Auyang (1995).
214 Auyang (2000).
215 Frankel (2004).
216 Way (2010).
217 Vákár (2011).
218 Marsh (2016).
Maudlin on fiber bundles:
If we adopt the metaphysics of the fiber bundle to represent chromodynamics, then we must reject the notion that quark color is a universal, or that there are color tropes which can be duplicates, or that quarks are parts of ‘natural sets’ which include all and only the quarks of the same color, for there is no fact about whether any two quarks are the same color or different. Further, we must reject the notion that there is any metaphysically pure relation of comparison between quarks at different points, since the only comparisons available are necessarily dependent on the existence of a continuous path in space-time connecting the points. So it seems that there are no color properties and no metaphysically pure internal relations between quarks. 219
219 Maudlin (2007), p. 96.
and
But if one asks whether, in this picture, the electromagnetic field is a substance or an instance of a universal or a trope, or some combination of these, none of the options seems very useful. If the electromagnetic field is a connection on a fiber bundle, then one understands what it is by studying fiber bundles directly, not by trying to translate modern mathematics into archaic philosophical terminology. 220
220 Maudlin (2007), p. 101.
7.7.1.3 Higher gauge theory
- Higher gauge field - nLab
- An ordinary gauge field is a field which is locally represented by a differential 1-form, the gauge potential, and whose field strength is locally a differential 2-form.
- Baez, J.C. & Muniain, J.P. (1994). Gauge Fields, Knots and Gravity. 221
- Baez, J.C. & Schreiber, U. (2005). Higher gauge theory. 222
- Baez, J.C. & Huerta, J. (2011). An invitation to higher gauge theory. 223
- Relationship to branes and string theory
7.7.1.4 Topological QFT
- Chern-Simons theory
- Chern-Simons theory - nLab
- Topological QFT (TQFT)
- Simon Donaldson and Edward Witten
- Witten, E. (1989). Quantum field theory and the Jones polynomial. 224
- Freed, D.S. (2001). Dirac charge quantization and generalized differential cohomology. 225
- Cobordism hypothesis - nLab
- Baez, J.C. & Stay, M. (2009). Physics, topology, logic, and computation: A Rosetta Stone. 226
- Schreiber, U. (2020). Differential cohomology in a cohesive \(\infty\)-topos. 227
See also:
- Category theory in the Outline on mathematics
- Differential geometry in the Outline on mathematics
7.7.2 Non-perturbative features
- Extended objects
- Sphalerons
- Instantons
- Q-balls
- Shifman, M. (2012). Advanced Topics in Quantum Field Theory: A lecture course. 230
- Manton, N.S. (2019). The inevitability of sphalerons in field theory. 231
- Percacci, R. (2024). Non-Perturbative Quantum Field Theory: An Introduction to Topological and Semiclassical Methods. 232
7.7.3 Supersymmetry
- Graded Lie algebras
- \(\mathbb{Z}/2\mathbb{Z}\)
- The supersymmetry algebra is a graded Lie algebra which closes under a combination of commutation and anti-commutation relations.
- Haag-Łopuszański-Sohnius theorem 233
- The unique loop-hole in the Coleman-Mandula theorem
- Deligne’s theorem on tensor categories
- Deligne, P. (2002). Catégories Tensorielles. 234
- Ostrik, V. (2004). Tensor categories (after Deligne). 235
- Schreiber, U. (2016). Learn about supersymmetry and Deligne’s theorem. 236
- Lepine, D. (2016). Deligne’s theorem on tensor categories. 237
- Deligne’s theorem on tensor categories - nLab
- Supersymmetry - nLab
- Superalgebra - Wikipedia
233 Haag, Łopuszański, & Sohnius (1975).
234 Deligne (2002).
235 Ostrik (2004).
236 Schreiber (2016b).
237 Lepine (2016).
Urs Schreiber:
not just that local spacetime supersymmetry is one possibility to have sensible particle content under Wigner classification, but that the class of (algebraic) super-groups precisely exhausts the moduli space of possible consistent local spacetime symmetry groups. 238
238 Schreiber (2016b).
nLab:
By Deligne’s theorem on tensor categories it is precisely the context of supersymmetry in which tensor categories over the complex numbers exhibit full Tannaka duality.
- Pedagogy
- Martin, S.P. (2016). A supersymmetry primer. 239
- Ellis, J. (2020). The Higgs, supersymmetry and all that. CERN Courier. January 10, 2020.
- Tong, D. (2022). Lectures on supersymmetric field theory. 240
- Bertolini, M. (2022). Lectures on supersymmetry. 241
- Minimal Supersymmetric Standard Model (MSSM)
- Dimopoulos, S. & Georgi, H. (1981). Softly broken supersymmetry and SU(5). 242
- Murayama, H. (2000). Supersymmetry_phenomenology. 243
- SUSY GUTs
- Supersymmetry allows unification of the couplings at the GUT scale.
- Arkani-Hamed, N., Cachazo, F., & Kaplan, J. (2008). What is the simplest quantum field theory?. 244
- Super division algebras
- Wall, C.T.C. (1964). Graded Brauer groups. 245
- Deligne, P. (1999). Notes on spinors. 246
- Freed, D.S. & Moore, G.W. (2012). Twisted equivariant matter. 247
- Geiko, R. & Moore, G.W. (2020). Dyson’s classification and real division superalgebras. 248
- Baez, J.C. (2020). The tenfold way. 249
- Associative real super division algebras
- Morita equivalence
- Supergravity
- Non-commutative geometry
- Connes, A. (1985). Non-commutative differential geometry. 253
239 S. P. Martin (2016).
240 Tong (2022).
241 Bertolini (2022).
242 Dimopoulos & Georgi (1981).
243 Murayama (2000).
244 Arkani-Hamed, Cachazo, & Kaplan (2008).
245 Wall (1964).
246 Deligne (1999).
247 Freed & Moore (2012).
248 Geiko & Moore (2020).
249 Baez (2020).
250 Freedman, Nieuwenhuizen, & Ferrara (1976).
251 van Nieuwenhuizen (1981).
252 Frè (2013), ch. 6.
253 Connes (1985).
See also:
7.8 Interpretations of quantum mechanics
The withdrawal of philosophy into a “professional” shell of its own has had disastrous consequences. The younger generation of physicists, the Feynmans, the Schwingers, etc., may be very bright; they may be more intelligent than their predecessors, than Bohr, Einstein, Schrödinger, Boltzmann, Mach and so on. But they are uncivilized savages, they lack in philosophical depth—and this is the fault of the very same idea of professionalism which you are now defending.
– from a letter in Appendix B of Feyerabend’s Against Method
- TODO: Maudlin 254
254 Maudlin (2019), p. TODO.
7.8.1 Measurement problem
- Maudlin, T. (1995). Three measurement problems. 255
- d’Espagnat, B. (1999). Conceptual Foundations of Quantum Mechanics. 256
- Schrödinger’s cat
- Video: Veritasium. (2020). Parallel worlds probably exist. Here’s why.
- Penrose: \(U\) and \(R\) operators
- Dürr, D. & Lazarovici, D. (2020). Understanding Quantum Mechanics: The World According to Modern Quantum Foundations. 257
- Mermin, N.D. (2022). A note on the quantum measurement problem. 258
7.8.2 Copenhagen “interpretation”
- Niels Bohr (1885-1962)
- Complementarity
- Reichenbach, H. (1944). Philosophic Foundations of Quantum Mechanics. 259
- Barad, K. (2007). Meeting the Universe Halfway: Quantum Physics and the Entanglement of Matter and Meaning. 260
- Some strange defenses of Bohr
- Becker, A. (2018). What is Real? 261
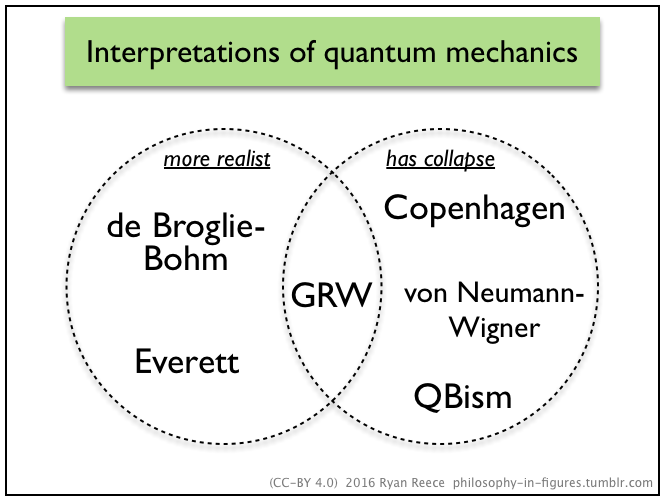
Criticisms:
- Collapse is arbitrary; \(U\) vs \(R\) operators; universal quantum theory \(\Rightarrow\) Everett.
- Complementarity is an arbitrary dualism.
- Not a real interpretation; Doesn’t say what there is.
- Bunge, M. (1955). Strife about complementarity (I). 262
- Bunge, M. (1955). Strife about complementarity (II). 263
7.8.4 EPR paradox
- Einstein, A., Podolsky, B. & Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete? 264
- Schrödinger, E. (1935). Discussion of probability relations between separated systems. 265
- coined entanglement
- Schrödinger, E. (1936). Probability relations between separated systems. 266
- Bohm, D. & Aharonov, Y. (1957). Discussion of experimental proof for the paradox of Einstein, Rosen, and Podolsky. 267
- Mermin, N.D. (1985). Is the moon there when nobody looks? 268
- Caulton, A. (2014). Physical entanglement in permutation-invariant quantum mechanics. 269
- Ismael, J. & Schaffer, J. (2020). Quantum holism: Nonseparability as common ground. 270
7.8.5 Von Neumann-Wigner interpretation
- Von Neumann-Wigner interpretation
- “consciousness causes collapse”
- Wigner’s friend
- Wigner, E.P. (1961). Remarks on the mind-body question. 271
- Deutsch, D. (1985). Quantum theory as a universal physical theory. 272
- Bong, K.W. et al. (2020). A strong no-go theorem on the Wigner’s friend paradox. 273
- Henry Stapp
- Roger Penrose
- Stacey, B.C. (2014). Von Neumann was not a quantum Bayesian. 274
Criticisms:
- Similar crticisms to Copenhagen: collapse is arbitrary; dualism of observables and observer.
- TODO: Discuss how Everett and his Ph.D. adviser, Wigner, disagreed about how to interpret the Wigner’s friend thought experiment.
7.8.6 Bell’s theorem
- Bell, J.S. (1964). On the Einstein Podolsky Rosen paradox. 275
- Bell, J.S. (1966). On the problem of hidden variables in quantum mechanics. 276
- Kochen, S. & Specker, E.P. (1967). The problem of hidden variables in quantum mechanics. 277
- Clauser, J., Horne, M., Shimony, A., & Holt, R. (1969). Proposed experiment to test local hidden-variable theories. 278
- Epistemological Letters (1973-1984)
- d’Espagnat, B. (1979). The quantum theory and reality. 279
- Aspect experiments (1982)
- Shimony, A. (1984). Contextual hidden variables theories and Bell’s inequalities. 280
- “experimental metaphysics”
- Bell, J.S. (1987). La Nouvelle Cuisine. 281
- GHZ experiment
- Greenberger, D., Horne, M.A., & Zeilinger, A. (1989). Going beyond Bell’s theorem. 282
- Greenberger, D., Horne, M.A., Shimony, A., & Zeilinger, A. (1990). Bell’s theorem without inequalities. 283
- Mermin, N.D. (1990). Quantum mysteries revisited. 284
- Gisin’s theorem 285
- Conway & Kochen’s “freewill theorem”
- Conway, J. & Kochen, S. (2006). The free will theorem. 286
- Maudlin, T. (2014). What Bell did. 287
- Ahmed, A., & Caulton, A. (2014). Causal decision theory and EPR correlations. 288
275 Bell (1964).
276 Bell (1966).
277 Kochen & Specker (1967).
278 Clauser, Horne, Shimony, & Holt (1969).
279 d’Espagnat (1979).
280 Shimony (1984).
281 Bell (2004b), pp. 232–248.
282 Greenberger, Horne, & Zeilinger (1989).
283 Greenberger, Horne, Shimony, & Zeilinger (1990).
284 Mermin (1990).
286 Conway & Kochen (2006).
287 Maudlin (2014).
288 Ahmed & Caulton (2014).
7.8.7 Bohmian mechanics
- de Broglie-Bohm theory
- version of quantum theory discovered by Louis de Broglie in 1927 and rediscovered by David Bohm in 1952.
- Bohm, D. (1952). A suggested interpretation of the quantum theory in terms of ‘hidden’ variables, I and II. 289
- Bohm, D. (1953). Proof that probability density approaches \(|\psi|^2\) in causal interpretation of quantum theory. 290
- Schönberg, M. (1954). On the hydrodynamical model of the quantum mechanics. 291
- Bohm, D. & Hiley, B.J. (1993). The Undivided Universe. 292
Discussion:
- Raman, V.V. & Forman, P. (1969). Why was it Schrödinger who developed de Broglie’s ideas?. 293
- Bell, J.S. (1987). Speakable and Unspeakable in Quantum Mechanics. 294
- Dürr, D., Goldstein, S., & Zanghì, N. (1995). Bohmian mechanics as the foundation of quantum mechanics 295
- Allori, V., Dürr, D., Goldstein, & Zanghì, N. (2002). Seven steps towards the classical world. 296
- Brown, M.R. & Hiley, B.J. (2004). Schrödinger revisited: An algebraic approach 297
- Dürr, D., Goldstein, S., & Zanghì, N. (2013). Quantum Physics Without Quantum Philosophy. Springer. 298
- Tumulka, R. (2017). Bohmian_mechanics. 299
- Del Santo, F. & Krizek, G.K. (2023). Against the “nightmare of a mechanically determined universe”: Why Bohm was never a Bohmian. 300
293 Raman & Forman (1969).
294 Bell (2004b).
295 Dürr, Goldstein, & Zanghì (1995).
296 Allori, Dürr, Goldstein, & Zanghì (2002).
297 Brown & Hiley (2004).
298 Dürr, Goldstein, & Zanghì (2013).
299 Tumulka (2017).
300 Del Santo & Krizek (2023).
Attempts at QFT:
- Bell, J.S. (1984). Beables for quantum field theory. 301
- Dürr, D., Goldstein, S., Tumulka, R., & Zanghì, N. (2004). Bohmian mechanics and quantum field theory. 302
- Dürr, D., Goldstein, S., Tumulka, R., & Zanghì, N. (2005). Bell-type quantum field theories. 303
- Dürr, D., Goldstein, S., Norsen, T., Struyve, W., & Zanghì, N. (2014). Can Bohmian mechanics be made relativistic?. 304
- Nikolić H. (2022). Relativistic QFT from a Bohmian perspective: A proof of concept. 305
301 Bell (1984).
302 Dürr, Goldstein, Tumulka, & Zanghì (2004).
303 Dürr, Goldstein, Tumulka, & Zanghì (2005).
304 Dürr, D. et al. (2014).
305 Nikolić (2022).
Attempts at empirical proposals:
- Das, S. & Dürr, D. (2019). Arrival time distributions of spin-1/2 particles. 306
- Stopp, F., Ortiz-Gutiérrez, L., Lehec, H., & Schmidt-Kaler, F. (2021). Single ion thermal wave packet analyzed via time-of-flight detection. 307
- Ananthaswamy, A. (2021). This simple experiment could challenge standard quantum theory. 308
306 Das & Dürr (2019).
307 Stopp, Ortiz-Gutiérrez, Lehec, & Schmidt-Kaler (2021).
308 Ananthaswamy (2021).
Primitive ontology:
- Esfeld, M., Lazarovici, D., Lam, V., & Hubert, M. (2017). The physics and metaphysics of primitive stuff. 309
- Reichert, P. & Lazarovici, D. (2022). The point of primitive ontology. 310
- TODO: Is primitive ontology really only used by Bohmians?
Virtues:
- No collapse; universal unitary Schrödinger evolution
- Consistent histories of particle trajectories.
Criticisms:
- Postulates a new theoretical apparatus, the guiding equation.
- Committed to particle onotology.
- Focuses on NRQM; Not yet demonstrated any relativistic extensions; No working QFT.
- Nonlocality baked right into the guiding equation.
- TODO: Ignores decoherence? Or if it doesn’t how naturally is it used?
- Ignores renormalization and EFT?
- TODO: Criticisms of primitive ontology as being apriori metaphysics.
- Caulton, A. (2018). A persistent particle ontology for quantum field theory. 311
- Deutsch: “Bohmian mechanics is Everett’s many worlds in denial.”
311 Caulton (2018).
7.8.8 Everettian interpretation
A theory containing many ad hoc constants and restrictions, or many independent hypotheses, in no way impresses us as much as one which is largely free of arbitrariness. 312
312 Everett (2012), p. 171.
- Schrödinger himself suggested in 1952 that the different terms of a superposition evolving under the Schrödinger equation are “not alternatives but all really happen simultaneously” (Wikipedia)
- Hugh Everett, III
- Everett, H. (1956). Theory of the Universal Wave Function. Ph.D. thesis. 313
- Everett, H. (1957). “Relative state” formulation of quantum mechanics. 314
- Wheeler, J.A. (1957). Assessment of Everett’s “relative state” formulation of quantum theory. 315
- Everett’s collected works 316
- Shikhovtsev, E. (2003). Biographical sketch of Hugh Everett, III.
- DeWitt, B.S. (1970). Quantum mechanics and reality. 317
- DeWitt, B.S. & Graham, N. (1973). The Many-Worlds Interpretation of Quantum Mechanics. 318
- Gell-Mann, M. & Hartle, J.B. (1989). Quantum mechanics in the light of quantum cosmology. 319
- Barrett, J.A. (2011). Everett’s pure wave mechanics and the notion of worlds. 320
- Barrett, J.A. (2016). Quantum worlds. 321
313 Everett (1956).
314 Everett (1957).
315 Wheeler (1957).
316 Everett (2012).
317 DeWitt (1970).
318 DeWitt & Graham (1973).
319 Gell-Mann & Hartle (1989).
320 Barrett (2011).
321 Barrett (2016).
It is therefore improper to attribute any less validity or “reality” to any element of a superposition than any other element, due to this ever present possibility of obtaining interference effects between the elements. All elements of a superposition must be regarded as simultaneously existing. 322
322 Everett (2012), p. 150.
- Everett’s later influence on the theory of decoherence
- Wallace, D. (2012). The Emergent Multiverse. 323
323 Wallace (2012).
A way out of this dilemma [the measurement problem] within quantum mechanical concepts requires one of two possibilities: a modification of the Schrödinger equation that explicitly describes a collapse (also called “spontaneous localization”), or an Everett type interpretation, in which all measurement outcomes are assumed to exist in one formal superposition, but to be perceived separately as a consequence of their dynamical autonomy resulting from decoherence. While this latter suggestion has been called “extravagant” (as it requires myriads of co-existing quasi-classical “worlds”), it is similar in principle to the conventional (though nontrivial) assumption, made tacitly in all classical descriptions of observation, that consciousness is localized in certain semi-stable and sufficiently complex subsystems (such as human brains or parts thereof) of a much larger external world. Occam’s razor, often applied to the “other worlds”, is a dangerous instrument: philosophers of the past used it to deny the existence of the interior of stars or of the back side of the moon, for example. So it appears worth mentioning at this point that environmental decoherence, derived by tracing out unobserved variables from a universal wave function, readily describes precisely the apparently observed “quantum jumps” or “collapse events” (as will be discussed in great detail in various parts of this book). 324
324 Joos, E. et al. (2003), p. 22.
- Barrett, J.A. (2019). The Conceptual Foundations of Quantum Mechanics. 325
- Carroll, S.M. & Singh, A. (2019). Mad-Dog Everettianism: Quantum mechanics at its most minimal. 326
- Carroll, S.M. (2019). Something Deeply Hidden.327
- Saunders, S. (2021). Branch-counting in the Everett interpretation of quantum mechanics. 328
- Wilhelm, I. (2022). Centering the Everett interpretation. 329
- Wallace, D. (2022). The sky is blue, and other reasons quantum mechanics is not underdetermined by evidence. 330
- Gisin, N. Del Santo, F. (2023). Towards a measurement theory in QFT: “Impossible” quantum measurements are possible but not ideal. 331
325 Barrett (2019).
326 Carroll & Singh (2019).
327 Carroll (2019).
328 Saunders (2021).
329 Wilhelm (2022).
330 Wallace (2022).
331 Gisin & Del Santo (2023).
Videos:
- Wallace, D. (2020). Many worlds of quantum theory. (9 mins)
- Carroll, S. (2022). The many worlds of quantum mechanics.
- Wallace, D. (2021). The sky is blue, and other reasons physics needs the Everett interpretation.
- Carroll, S. (2023). The many worlds of quantum mechanics.
Virtues:
- Minimal; No additions to quantum theory
- No collapse; universal unitary Schrödinger evolution
- Relativistic QFT works naturally.
- Decoherence does a lot of work at explaining the appearance of collapse into classical states.
- Classical concepts are derived; not dual; no complementarity.
- Applies QM to the system + aparatus + observer.
- First interpretation to allow for quantum cosmology, the quantum mechanics of the universe as a closed system.
Criticisms:
- It seems to clash with the manifest image and the human condition.
- There are too many worlds.
- Boughn, S. (2018). Making sense of the many worlds interpretation. 332
- Frauchiger, D. & Renner, R. (2018). Quantum theory cannot consistently describe the use of itself. 333
- Bub, J. (2019). ‘Two Dogmas’ redux. 334
- Barbado, L.C. & Del Santo, F. (2023). On playing gods: The fallacy of the many-worlds interpretation. 335
See also:
7.8.9 Collapse interpretations
- Ghirardi-Rimini-Weber theory (GRW) 336
- TODO: find ref that GRW is empirical
- Ghirardi, G.C., Pearle, P., Rimini, A. (1990). Markov processes in Hilbert space and continuous spontaneous localization of systems of identical particles. 337
- Bassi, A. (2005). Collapse models: analysis of the free particle dynamics. 338
- Putnam, H. (1965). A philosopher looks at quantum mechanics. 339
- Putnam, H. (2005). A philosopher looks at quantum mechanics (again). 340
- Wuthrich, C. (2014). Putnam looks at quantum mechanics (again and again). 341
- Allori, V. (2022). What is it like to be a relativistic GRW theory? Or: Quantum mechanics and relativity, still in conflict after all these years. 342
336 Ghirardi, Rimini, & Weber (1986).
337 Ghirardi, Pearle, & Rimini (1990).
338 Bassi (2005).
339 Putnam (1975).
340 Putnam (2005).
341 Wuthrich (2014).
342 Allori (2022).
Virtues:
- Tries to explain collapse stochastically.
Criticisms:
- Collapse is arbitrary; \(U\) vs \(R\) operators
- Ignores decoherence?
- TODO: Look into how GRW can be relativistic. QFT?
- Tegmark, M. (1993). Apparent wave function collapse caused by scattering. 343
343 Tegmark (1993).
7.8.10 Epistemic interpretations
- \(\psi\)-epistemic interpretations
- Quantum Bayesianism (QBism)
- Caves, C.M., Fuchs, C.A., & Schack, R. (2001). Quantum probabilities as Bayesian probabilities. 344
- Fuchs, C.A. (2002). Quantum mechanics as quantum information (and only a little more). 345
- Fuchs, C.A. (2010). QBism, the perimeter of quantum Bayesianism. 346
- Fuchs, C.A. & Schack, R. (2013). Quantum-Bayesian coherence: The no-nonsense version. 347
- Fuchs, C.A., Mermin, N.D., & Schack, R. (2014). An introduction to QBism with an application to the locality of quantum mechanics. 348
- Fuchs, C.A. & Stacey, B.C. (2016). QBism: Quantum theory as a hero’s handbook. 349
- Harrigan, N., & Spekkens, R.W. (2010). Einstein, incompleteness, and the epistemic view of quantum states. 350
- Leifer, M.S. & Spekkens, R.W. (2013). Towards a formulation of quantum theory as a causally neutral theory of bayesian inference. 351
344 Caves, Fuchs, & Schack (2001).
345 Fuchs (2002).
346 Fuchs (2010).
347 Fuchs & Schack (2013).
348 Fuchs, Mermin, & Schack (2014).
349 Fuchs & Stacey (2016).
350 Harrigan & Spekkens (2010).
351 Leifer & Spekkens (2013).
Criticisms:
- Anti-Copernican; anthropomorphism
- PBR theorem
- Ignores decoherence?
7.8.11 PBR theorem
- Pusey, M.F., Barrett, J., & Rudolph, T. (2012). On the reality of the quantum state. 352
- Wikipedia: Either the quantum state corresponds to a physically real object and is not merely a statistical tool, or else all quantum states, including non-entangled ones, can communicate by action at a distance.
- Leifer, M.S. (2011). Can the quantum state be interpreted statistically?
- Schlosshauer, M. & Fine, A. (2012). Implications of the Pusey-Barrett-Rudolph quantum no-go theorem. 353
- Wallace, D. (2013). Inferential vs dynamical conceptions of physics. 354
- Nigg, D. et al. (2015). Can different quantum state vectors correspond to the same physical state? An experimental test. 355
- Ontological vs nomological interpretations of wavefunctions
352 Pusey, Barrett, & Rudolph (2012).
353 Schlosshauer & Fine (2012).
354 Wallace (2013).
355 Nigg, D. et al. (2015).
Videos:
- Maudlin, T. (2021). The PBR theorem, quantum state realism, and statistical independence.
7.8.12 Other interpretations
- Transactional quantum mechanics
- Invariant set theory
- Palmer, T.N. (2009). The invariant set postulate: A new geometric framework for the foundations of quantum theory and the role played by gravity. 358
- Palmer, T.N. (2016). Invariant set theory. 359
- Cellular automaton
- ’t Hooft, G. (2014). The cellular automaton interpretation of quantum mechanics. 360
- Relational quantum mechanics
- Martin-Dussaud, P., Rovelli, C., & Zalamea, F. (2018). The notion of locality in relational quantum mechanics. 361
- Superdeterminism
- ’t Hooft, G. (2021). An unorthodox view on quantum mechanics. 362
- Hossenfelder, S. & Palmer, T. (2020). Rethinking superdeterminism. 363
- Taxonomies
- Adlam, E., Hance, J.R., Hossenfelder, S., & Palmer, T.N. (2023). Taxonomy for physics beyond quantum mechanics. 364
- Hossenfelder, S. (2023). Quantum confusions, cleared up (or so I hope). 365
- Misc
- Del Santo, F., Schwarzhans, E. (2022). “Philosophysics” at the University of Vienna: The (Pre-)history of foundations of quantum physics in the Viennese cultural context. 366
356 Cramer (1986).
357 Maudlin (1996).
358 Palmer (2009).
359 Palmer (2016).
360 ’t Hooft (2014).
361 Martin-Dussaud, Rovelli, & Zalamea (2018).
362 ’t Hooft (2021).
363 Hossenfelder & Palmer (2020).
364 Adlam, Hance, Hossenfelder, & Palmer (2023).
365 Hossenfelder (2023).
366 Del Santo & Schwarzhans (2022).
From Sabine Hossenfelder, some examples for models that violate measurement independence are here:
- Brans , C.H. (1988). Bell’s theorem does not eliminate fully causal hidden variables. 367
- Palmer, T.N. (1995). A local deterministic model of quantum spin measurement. 368
- Degorre, J., Laplante, S., & Roland, J. (2005). Simulating quantum correlations as a distributed sampling problem. 369
- Hall, M.J.W. (2010). Local deterministic model of singlet state correlations based on relaxing measurement independence. 370
- Ciepielewski, G.S, Okon, E., & Sudarsky, D. (2020). On superdeterministic rejections of settings independence. 371
- Donadi, S. & Hossenfelder, S. (2022). A toy model for local and deterministic wave-function collapse. 372
7.8.13 Bad takes
- MIT Technology Review. (2019). A quantum experiment suggests there’s no such thing as objective reality.
- Proietti, M. et al. (2019). Experimental test of local observer independence. 373
- Weinberg, J. et al. (2019). Philosophers on a physics experiment that “suggests there’s no such thing as objective reality”. Daily Nous. March 21, 2019.
- Nikolić, H. (2007). Quantum mechanics: Myths and facts. 374
Press release for The Nobel Prize in Physics 2022:
This means that quantum mechanics cannot be replaced by a theory that uses hidden variables.
which is wrong! The violation of Bell’s inequality means that QM cannot be explained by fully local hidden variables. Bohmian mechanics exists as a counter example that hidden variables can explain QM, but require a non-local guiding equation.
7.9 The standard model of particle physics
7.9.1 History of particle physics
- Particle physics
- Particle accelerator
- Ernest Rutherford (1871-1937)
- Rolf Widerøe (1902-1996)
- Lawrence Berkeley National Laboratory (est. 1931)
- Ernest Lawrence (1901-1958)
- Luis Walter Alvarez (1911-1988)
- Brookhaven National Laboratory (est. 1947)
- Murray Gell-Mann (1929-2019)
- First Review of Particle Physics (1957)
- Review of Particle Physics 375
- European Organization for Nuclear Research (CERN) (est. 1954)
- Carlo Rubbia (b. 1934)
- SLAC National Accelerator Laboratory (est. 1962)
- \(J/\psi\) meson - “November Revolution” (1974)
- Fermilab (est. 1969)
- Robert R. Wilson (1914-2000)
- Physics Problems for the Next Millennium
375 Zyla, P.A. et al. (Particle Data Group) (2021).
7.9.2 Mixing
- Cabibbo angle (1963) 376
- CP violation
- CKM matrix
- Kaons
- B-mesons
376 Cabibbo (1963).
7.9.3 Higgs mechanism
In 1964, three groups: Robert Brout and Francois Englert 377; Peter Higgs 378; and Gerald Guralnik, Carl R. Hagen, and Tom Kibble 379, independently demonstrated an exception to Goldstone’s theorem, showing that Goldstone bosons do not occur when a spontaneously broken symmetry is local. Instead, the Goldstone mode provides the third polarization of a massive vector field, resulting in massive gauge bosons. The other mode of the original scalar doublet remains as a massive spin-zero particle, the Higgs boson. This is the Englert-Brout-Higgs-Guralnik-Hagen-Kibble mechanism, or Higgs mechanism. In the Standard Model, the Higgs boson also couples to the fermions, generating their bare masses.
- Georgi, H. (1982). Is the Higgs real? 380
- Lyre, H. (2008). Does the Higgs mechanism exist? 381
380 Georgi (1999), p. 280.
381 Lyre (2008).
382 ATLAS Collaboration (2012).
383 CMS Collaboration (2012).
On July 4 of 2012, the ATLAS 382 and CMS 383 experiments both announced discovering a new particle consistent with the long-sought-after Higgs boson, a key to explaining electroweak symmetry breaking in the Standard Model of particle physics.
- Cao, T.Y. (2016). The Englert-Brout-Higgs mechanism: An unfinished project. 384
- ’t Hooft, G. (2022). A triumph for theory.
384 T. Y. Cao (2016).
7.9.4 A model of leptons
- Glashow, S. (1961). Partial symmetries of weak interactions. 385
- Weinberg, S. (1967). A model of leptons. 386
- Salam, A. & Ward, J.C. (1964). Gauge theory of elementary interactions. 387
- Salam, A. & Ward, J.C. (1964). Electromagnetic and weak interactions. 388
- GWS electroweak theory: SU(2) \(\times\) U(1)
- Weinberg, S. (1979). Conceptual foundations of the unified theory of weak and electromagnetic interactions. Nobel Lecture, December 8, 1979. 389
- UA1 and UA2 Collaborations discovered the \(W\) and \(Z\) bosons in 1983.
- Rubbia, C. (1984). Experimental observation of the intermediate vector bosons \(W^{+}\), \(W^{-}\), and \(Z^{0}\). Nobel lecture, December 8, 1984. 390
- Chalmers, M. (2017). Model physicist. (CERN Courier about Weinberg) 391
- Woit, P. (2022). Glashow interview.
7.9.5 Quantum chromodynamics
- QCD: SU(3)
- SU(3) \(\times\) SU(2) \(\times\) U(1)
- Asymptotic freedom
- Anzivino, C., Vaibhav, V. & Zaccone, A. (2024). Random close packing of binary hard spheres predicts the stability of atomic nuclei. 392
392 Anzivino, Vaibhav, & Zaccone (2024).
7.9.6 Three generations of fermions
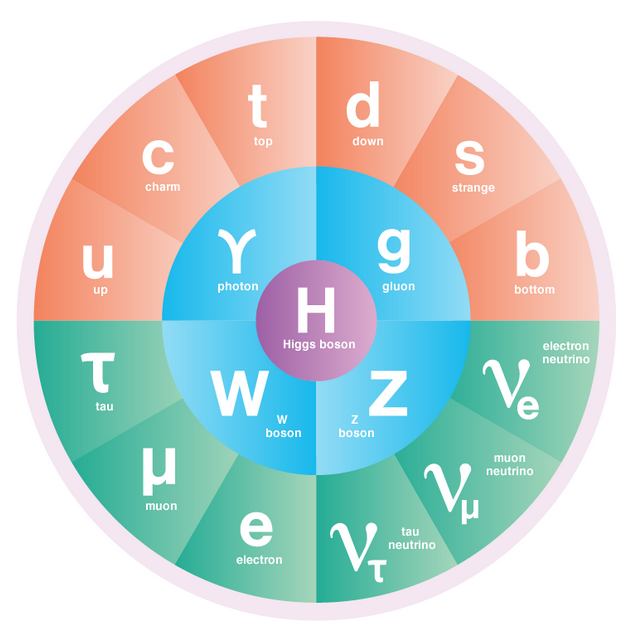
- Discovery of charm: “November revolution” at SLAC and BNL (1974)
- Discovery of tau at SLAC + LBL (1975)
- Discovery of bottom at Fermilab (1977)
- Discovery of three neutrino generations from the \(Z\) width at LEP (1989)
- Discovery of top at Fermilab (1995)

More:
- Nima Arkani-Hamed doing particle physics a priori: “Why is there a Macroscopic Universe?”
- Nima Arkani-Hamed on Collider Physics from the Bottom Up
7.9.7 Experimental methods
- Hamamatsu. (2007). Photomultiplier Tubes: Basics and Applications. 393
393 Hamamatsu (2007).
7.10 Beyond the standard model
- Beyond the standard model (BSM)
7.10.1 Neutrino masses
- Introduction
- Neutrino masses and mixings
- PMNS matrix and CP-violation
- Are neutrinos Marojana or Dirac fermions?
- Seesaw mechanism
- Solar neutrino problem
- Homestake experiment (1964-1968)
- Raymond Davis Jr. (1914-2006)
- Super-Kamiokande (1998)
- Sudbury Neutrino Observatory (1999-2006)
- Homestake experiment (1964-1968)
- LSND anomaly
- Vitagliano, E., Tamborra, I., & Raffelt, G. (2020). Grand unified neutrino spectrum at Earth: Sources and spectral components. 398
7.10.2 Ad hoc structures
- Why SU(3) \(\times\) SU(2) \(\times\) U(1)?
- Strong \(CP\) problem
- Axions
- Matter-antimatter asymmetry
- 3 generations
- Hierarchy problem(s)
- Dark matter and dark energy
See also:
7.10.3 Experimental anomalies
- Ultra-high-energy cosmic rays
- Greisen-Zatsepin-Kuzmin (GZK) limit
- Pierre Auger Collaboration 399
- LSND anomaly, again
- PRL. (2016). Theorists react to the CERN 750 GeV diphoton data.
- Garisto, D. (2018). The era of anomalies.
- Lepton universality at LHCb
- LHCb Collaboration. (2021). Test of lepton universality in beauty-quark decays.
- LHCb Collaboration. (2021). Tests of lepton universality using \(B^{0}\rightarrow{}K^{0}_{S}\ell^{+}\ell^{-}\) and \(B^{+}\rightarrow{}K^{*+}\ell^{+}\ell^{-}\) decays.
- Muon \(g-2\)
- Capdevilla, R., Curtin, D., Kahn, Y., & Krnjaic, G. (2021). A no-lose theorem for discovering the new physics of \((g-2)_\mu\) at muon colliders. 400
- Aimè, C. et al. (2022). Muon collider physics summary. 401
- \(W\) mass
7.10.4 Grand unification
- Running of the couplings
- Supersymmetry
- Baez, J.C. & Huerta, J. (2009). Division algebras and supersymmetry I. 403
- Baez, J.C. & Huerta, J. (2010). Division algebras and supersymmetry II. 404
- Grand Unified Theories (GUTs)
- Pati & Salam 405
- Georgi & Glashow 406
- Georgi, H., Quinn, H.R., & Weinberg, S. (1974). Hierarchy of interactions in unified gauge theories. 407
- Slansky 408
- Georgi, H. (1982). Lie Algebras in Particle Physics. 409
- Baez, J.C. & Huerta, J. (2009). The algebra of grand unified theories. 410
- Lisi, A.G. (2007). An exceptionally simple theory of everything. 411
- Chester, D., Marrani, A., & Rios, M. (2023). Beyond the Standard Model with six-dimensional spinors. 412
403 Baez & Huerta (2009a).
404 Baez & Huerta (2010).
405 Pati & Salam (1974).
406 Georgi & Glashow (1974).
407 Georgi, Quinn, & Weinberg (1974).
408 Slansky (1981).
409 Georgi (1999).
410 Baez & Huerta (2009b).
411 Lisi (2007).
412 Chester, Marrani, & Rios (2023).
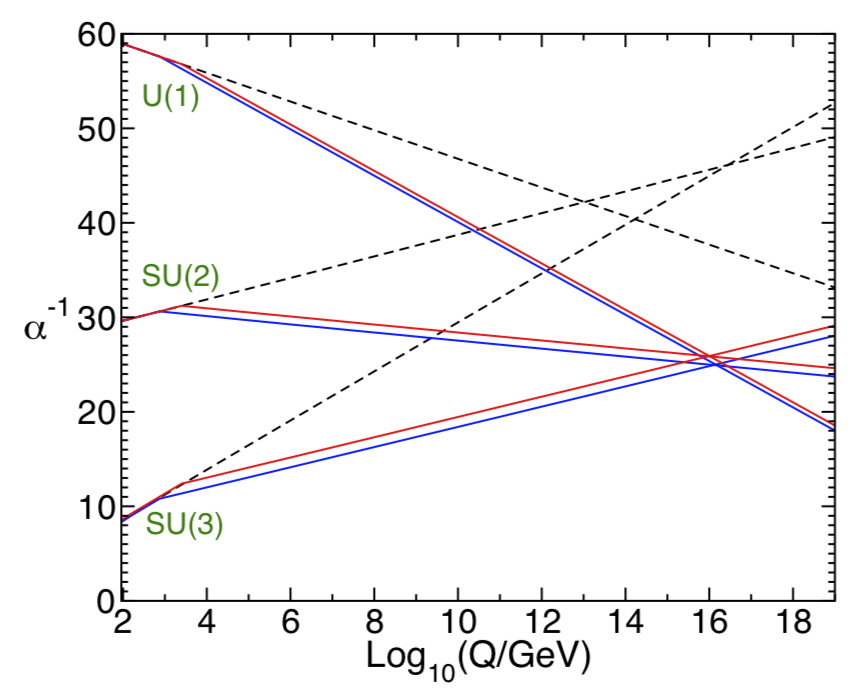
413 S. P. Martin (2016), p. 66.
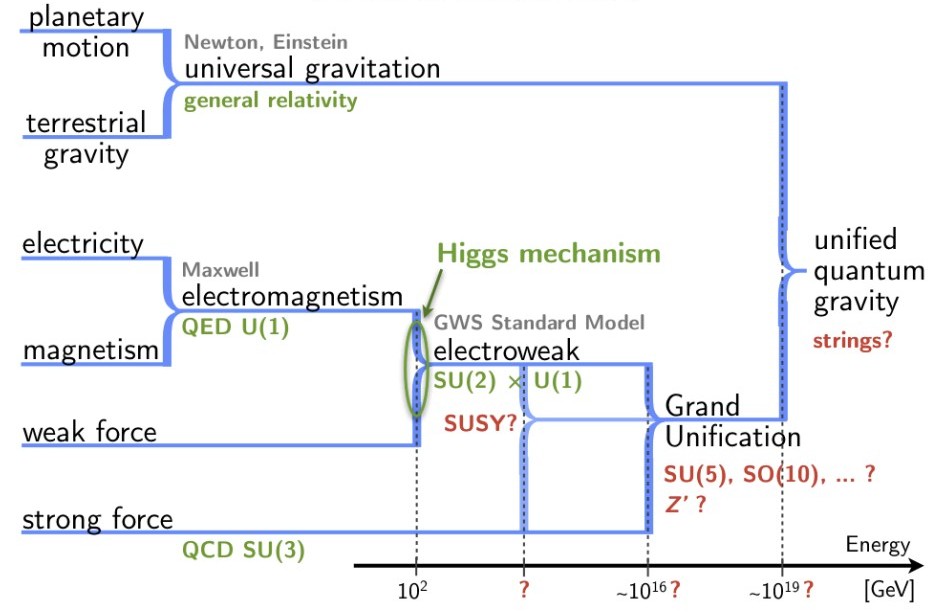
See also:
7.10.5 Baryogenesis
- Matter-antimatter asymmetry
- Dine, M. & Kusenko, A. (2004). The origin of the matter-antimatter asymmetry. 414
414 Dine & Kusenko (2004).
7.10.6 Future colliders and criticisms
- Baggot, J. (2013). Farewell to Reality. 415
- CERN. (2020). Press Release: Particle physicists update strategy for the future of the field in Europe. (“FCC”)
- Hossenfelder, S. (2020). The world doesn’t need a new gigantic particle collider.
415 Baggott (2013).
7.10.7 Quantum gravity
- Strings
- Candelas, P., Horowitz, G.T., Strominger, A., & Witten, E. (1985). Vacuum configurations for superstrings. 416
- Start of string phenomenology
- Candelas, P., Horowitz, G.T., Strominger, A., & Witten, E. (1985). Vacuum configurations for superstrings. 416
- AdS/CFT
- Maldacena, J.M. (1998). The large \(N\) limit of superconformal field theories and supergravity. 417
- Witten, E. (1998). Anti-de Sitter space and holography. 418
- Polyakov, A.M. (2008). From quarks to strings. 419
- Gauge-string duality
- Gopakumar, R. (2011). What is the simplest gauge-string duality?. 420
- Gopakumar, R. & Mazenc, E.A. (2022). Deriving the simplest gauge-string duality, I: Open-closed-open triality. 421
- Emergence of spacetime
- Penrose, R. (1971). Angular momentum: an approach to combinatorial spacetime. 422
- Ney, A. (2021). From quantum entanglement to spatiotemporal distance. 423
7.11 Gravity and cosmology
7.11.1 General relativity
- Recall Special relativity.
- Bernhard Riemann (1826-1866)
- Einstein, A. & Grossmann, M. (1913). Outline of a generalized theory of relativity and of a theory of gravitation. 424
- Misner, C.W., Thorne, K.S., & Wheeler, J.A. (1973). Gravitation. 425
- Carroll, S.M. (2004). Spacetime and Geometry. 426
- Arntzenius, F. (2012). Space, Time, and Stuff. 427
- General covariance, diffeomorphism invariance, background independence
- Norton, J.D. (1993). General covariance and the foundations of general relativity: Eight decades of dispute. 428
424 Einstein & Grossmann (1913).
425 Misner, Thorne, & Wheeler (1973).
426 Carroll (2004).
427 Arntzenius (2012).
428 Norton (1993).
\[ R_{\mu\nu} - \frac{1}{2} R \: g_{\mu\nu} + \Lambda \: g_{\mu\nu} = \frac{8 \pi G}{c^4} \: T_{\mu\nu} \]
7.11.2 Newtonian gravity
- History of Newton and calculus.
- Newtonian gravity is the right law to conserve gravitational force flux in three dimensions.
- Derive Newtonian gravity as the low-velocity, low-curavature limit of GR.
- Toth, V.T. (2016). The Newtonian limit in general relativity.
7.11.3 Big bang model
- Alexander Friedmann solves the Einstein field equations for an expanding universe in 1922.
- Edwin Hubble discovered that our galaxy is one of many in 1923.
- Georges Lemaître independently solved the Einstein field equations in 1927.
- Edwin Hubble observationally confirmed the expansion of the universe in 1929.
- Arno Penzias and Robert Wilson discovered the cosmic background radiation (CMB) in 1964.
- See history reviewed by Frè 429
- The First Three Minutes 430
- Ryden, B. (2003). Introduction to Cosmology. 431
- Big Bang Nucleosynthesis (BBN)
- Bahcall, N.A., Ostriker, J.P., Perlmutter, S., & Steinhardt, P.J. (1999). The cosmic triangle: Revealing the state of the universe. 432
7.11.4 Spacetime
- Substantivalism vs relationism
- Berkeley, G. (1721). De Motu.
- Leibniz, Mach, Barbour
- Romero, G.E. (2015). On the ontology of spacetime: Substantivalism, relationism, eternalism, and emergence. 433
- Video: A mock debate on time with Julian Barbour and Tim Maudlin (2011).
433 Romero (2015).
7.11.5 Blackholes
- Penington, G. (2019). Entanglement wedge reconstruction and the information paradox. 434
434 Penington (2019).
7.11.6 Gravitational waves
- Poincaré
- Einstein
- Hulse-Taylor binary pulsar
- LIGO
- Multi-messenger astronomy
- NANOGrav
7.11.7 Dark matter
- Bullet Cluster
- “A direct empirical proof of the existence of dark matter” 435
- Galaxy formation
- Millennium Simulation
- WIMP Miracle
- Disfavored by LHC thus far.
- Bahcall, N.A. (2015). Dark matter universe. 436
- Howe, A.R. (2019). The dark matter flowchart, annotated.
- Arbey, A. & Mahmoudi, F. (2021). Dark matter and the early Universe: a review. 437
- Martens, N. (2022). Dark matter realism. 438
- Boyd, N.M., De Baerdemaeker, S., Heng, K., & Matarese, V. (Eds.). (2023). Philosophy of Astrophysics.
7.11.8 Inflation
- Cosmological constant problem
- Proposed by Alan Guth in 1979.
- Guth, A.H. (1981). Inflationary universe: A possible solution to the horizon and flatness problems. 440
- Albrecht, A. & Steinhardt, P.J. (1982). Cosmology for Grand Unified Theories with radiatively induced symmetry breaking. 441
- Linde, A.D. (1982). A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. 442
- False vaccuum from inflaton field
- Slow-roll of inflaton field value solved the “graceful exit” problem of ending inflation.
- Baumann, D. (2009). TASI lectures on inflation. 443
- Eternal inflation
- Steinhardt, P.J. (1983). Natural inflation. 444
- Linde, A.D. (1983). Chaotic inflation. 445
- Guth, A.H. (2007). Eternal inflation and its implications. 446
- Discovery of dark energy
- TODO
- \(\Lambda\)-CDM Cosmological Standard Model
439 J. Martin (2012).
440 Guth (1981).
441 Albrecht & Steinhardt (1982).
442 Linde (1982).
443 Baumann (2009).
444 Steinhardt (1983).
445 Linde (1983).
446 Guth (2007).
Guth:
The peculiar properties of the false vacuum stem from its pressure, which is large and negative… Mechanically such a negative pressure corresponds to a suction, which does not sound like something that would drive the Universe into a period of rapid expansion. The mechanical effects of pressure, however, depend on pressure differences, so they are unimportant if the pressure is reasonably uniform. According to general relativity, however, there is a gravitational effect that is very important under these circumstances. Pressures, like energy densities, create gravitational fields, and in particular a positive pressure creates an attractive gravitational field. The negative pressure of the false vacuum, therefore, creates a repulsive gravitational field, which is the driving force behind inflation. 447
447 Guth (1997).
7.11.9 Alternative theories of gravity
- Einstein-Cartan theory
- Modified Newtonian dynamics (MOND)
- TODO: Sabine Hossenfelder
- Entropic gravity
7.12 Fine-tuning
- Fine-tuning and naturalness
- Anthropic principle
- TODO: Find Weinberg on AP and naturalness
- Relationship to evolution
- Richard Dawkins and Steven Weinberg discuss science and religion
- Meta-stability of the Higgs vaccuum in \(m_t\) vs \(m_H\)
7.13 Complexity and emergence
- nonlinear systems
- chaos
- Universality
- Thermodynamics, statistical mechanics, renormalization.
- Simon, H.A. (1962). The architecture of complexity. Proceedings of the American Philosophical Society, 106, 467–482. 449
- Anderson, P.W. (1972). More is different. 450
- Berry, M. (1979). Evolution of semiclassical quantum states in phase space. 451
- Berry, M. (1983). Semiclassical mechanics of regular and irregular motion. 452
- Gell-Mann, M. (1988). Simplicity and complexity in the description of nature. 453
- Bedau, M.A. (1997). Weak emergence. 454
- Bunge, M. (2001). Philosophy in Crisis: The Need for Reconstruction.
- Emergence 455
- DeDeo, S. (2012). Video: Lecture 1: Coarse-graining, renormalization & universality.
- Lisi, A.G. (2017). Emergence. 456
- Bain
- TODO
- Jardón, R. (2020). Emergence.
- Views on reductionism
- Video: Closer To Truth: What’s Strong Emergence?
- George F. R. Ellis vs Barry Loewer
- John, Y.J. (2020). An emergence reading list.
449 H. A. Simon (1962).
450 Anderson (1972).
451 Berry (1979).
452 Berry (1983).
453 Gell-Mann (1988).
454 Bedau (1997).
455 Bunge (2001), p. 72.
456 Lisi (2017).
Anderson:
The ability to reduce everything to simple fundamental laws does not imply the ability to start from those laws and reconstruct the universe. The constructionist hypothesis breaks down when confronted with the twin difficulties of scale and complexity. At each level of complexity entirely new properties appear. Psychology is not applied biology, nor is biology applied chemistry. We can now see that the whole becomes not merely more, but very different from the sum of its parts. 457
457 Anderson (1972), p. 393.
See also:
7.14 Bracketing human experience
- entailment, reductionism
- crossing symmetry in QFT
- Bokulich, P. (2011). Hempel’s dilemma and domains of physics. 458 Acceptance speech for the FFRF’s the emperor has no clothes award.
- Carroll, S. (2015). Quantum field theory and the limits of knowledge.
- Carroll, S. (2021). The quantum field theory on which the everyday world supervenes.
458 Bokulich (2011).

Videos of talks:
- Carroll, S. (2013). Poetic Naturalism.
- Carroll, S. (2014). Has science refuted religion?
- Carroll, S. & Wallace, A. (2017). The Nature of Reality: A Dialogue Between a Buddhist Scholar and a Theoretical Physicist.
- Carroll, S. (2022). Quantum Field Theory and the Limits of Knowledge.
See also:
- Physicalism in the Outline on naturalism
7.15 My thoughts
- Sean Carroll QM: what there is, is more than we can see.
- Reece, R. (2017). Quora: What is currently the best explanation for how and why the quantum wave function collapses?
7.16 Annotated bibliography
7.16.1 Einstein, A., Podolsky, B. & Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete?
- Einstein et al. (1935)
7.16.1.1 My thoughts
- TODO.
7.16.2 Anderson, P. (1972). More is different.
- Anderson (1972)
7.16.2.1 My thoughts
- TODO.
7.16.3 Redhead, M. (1988). A philosopher looks at quantum field theory.
- Redhead (1988)
7.16.3.1 My thoughts
- TODO.
7.16.4 Joos, E., Zeh, H.D., Kiefer, C., Kupsch, J., Stamatescu, I.O. (2003). Decoherence and the Appearance of a Classical World in Quantum Theory.
- Joos, E. et al. (2003).
7.16.4.1 My thoughts
- TODO.
7.16.5 Pusey, M.F., Barrett, J., & Rudolph, T. (2012). On the reality of the quantum state.
- Pusey et al. (2012)
- arxiv:1111.3328
7.16.5.1 My thoughts
- TODO.
7.16.6 More articles to do
7.17 Links and encyclopedia articles
7.17.1 SEP
- Being and Becoming in Modern Physics
- Bell’s Theorem
- Bohmian Mechanics
- Boltzmann’s Work in Statistical Physics
- Chaos
- Collapse Theories
- Computer Simulations in Science
- Copenhagen Interpretation of Quantum Mechanics
- Decoherence
- Emergent Properties
- Everett’s Relative-State Formulation of Quantum Mechanics
- Fine-tuning
- General relativity, Early philosophical interpretations of
- Holism and Nonseparability in Physics
- Identity and Individuality in Quantum Theory
- Identity of Indiscernibles
- Kochen-Specker Theorem
- Many-Worlds Interpretation of Quantum Mechanics
- Modal Interpretations of Quantum Mechanics
- Measurement in Quantum Theory
- Philosophical Issues in Quantum Theory
- Poincaré, Henri (1854-1912)
- Quantum-Bayesian and Pragmatist Views of Quantum Theory
- Quantum Entanglement and Information
- Quantum Field Theory
- Quantum Field Theory, History of
- Quantum Gravity
- Quantum Logic and Probability Theory
- Quantum Mechanics
- Quantum Theory: von Neumann vs Dirac
- Relational Quantum Mechanics
- Statistical mechanics, Philosophy of
- Supertasks
- Symmetry and Symmetry Breaking
- Time
- Weyl, Hermann (1885-1955)
7.17.2 IEP
7.17.3 Scholarpedia
- Algebraic renormalization
- ATLAS experiment
- Bjorken scaling
- Coleman-Mandula theorem
- Coleman-Weinberg mechanism
- CP violation in electroweak interactions
- Critical Phenomena: field theoretical approach
- Daya Bay Experiment
- Englert-Brout-Higgs-Guralnik-Hagen-Kibble mechanism
- Englert-Brout-Higgs-Guralnik-Hagen-Kibble mechanism (history)
- Faddeev-Popov ghosts
- Gauge invariance
- Gauge theories
- Glashow-Iliopoulos-Maiani mechanism
- Grand unification
- Lagrangian formalism for fields
- Lattice gauge theories
- Lattice quantum field theory
- Leptogenesis
- Local operator
- MS-bar definition of parton distribution functions
- Multiloop Feynman integrals
- Operator product expansion
- Parton shower Monte Carlo event generators
- Path integral
- Path integral: mathematical aspects
- Principle of least action
- QCD evolution equations for parton densities
- Second quantization
- Symmetry breaking in classical systems
- Wightman quantum field_theory
7.17.4 Wikipedia
- AdS/CFT correspondence
- Aharonov-Bohm effect
- Ampère, André-Marie (1775-1836)
- Atomism
- Background independence
- Bargmann, Valentine (1908-1989)
- Bargmann-Wigner equations
- Beeckman, Isaac (1588-1637)
- Bell’s theorem
- Bekenstein bound
- Black hole information paradox
- Bohm, David (1917-1992)
- Bohr, Niels (1885-1962)
- Bohr-Einstein debates
- Born rule
- Bullet Cluster
- C*-algebra
- Casimir effect
- Cauchy, Augustin-Louis (1789-1857)
- Causal Processes
- Causal perturbation theory
- Central limit theorem
- Causality
- CHSH inequality
- Chronology of the universe
- Church-Turing-Deutsch principle
- Church-Turing thesis
- Clinamen
- Complexity
- Constructor theory
- Corpuscularianism
- CP violation
- Curie’s Principle
- de Broglie, Louis (1892-1987)
- De Broglie-Bohm theory
- Democritus (c. 460-370 BCE)
- Descartes, René (1596-1650)
- Determinism
- Digital philosophy
- Digital physics
- Effective field theory
- Einselection
- Equivalence principle
- Emergence
- Entropic gravity
- Entropy
- Entropy, Introduction to
- Epicurus (341-270 BCE)
- Equipartition theorem
- Erlangen program
- Eternalism (philosophy of time)
- Franklin, Benjamin (1706-1790)
- Fraunhofer, Joseph von (1787-1826)
- Four-dimensionalism
- Field
- Firewall
- Gauss, Carl Friedrich (1777-1855)
- Gelfand-Naimark theorem
- Gelfand-Naimark-Segal construction
- General relativity
- Ghirardi-Rimini-Weber theory
- Gibbs, Josiah Willard (1839-1903)
- Grand Unified Theory
- Haag, Rudolf (1922-2016)
- Haag-Łopuszański-Sohnius theorem
- Haag’s theorem
- Hidden variable theory
- Hierarchy problem
- Hilbert, David (1862-1943)
- Hilbert space
- Holographic principle
- Holomovement
- Holonomy
- Kaluza-Klein theory
- Kanada (c. 600-100 BCE)
- Kochen-Specker Theorem
- Lambda-CDM model
- Landau pole
- Leucippus (fl. 5th century BCE)
- Little hierarchy problem
- Locality, Principle of
- Local hidden variable theory
- Local (algebraic) quantum field theory
- Loopholes in Bell test experiments
- Lucretius (c. 99-55 BCE)
- Mach’s principle
- Measurement in quantum mechanics
- Measurement problem
- M-theory
- M-theory, Introduction to
- Mu problem
- No-cloning theorem
- Noether, Emmy (1882-1935)
- Noether’s theorem
- Objective collapse theory
- Particle physics
- Particle physics and representation theory
- PBR theorem
- Physical cosmology
- Physicalism
- Physics, Philosophy of
- Poincaré, Henri (1854-1912)
- Poincaré group
- Quantization
- Quantization, Canonical
- Quantization, Geometric
- Quantum decoherence
- Quantum entanglement
- Quantum field theory
- Quantum gravity
- Quantum mechanics
- Quantum mechanics, Mathematical formulation of
- Quantum triviality
- Reeh-Schlieder theorem
- Regularization
- Relational quantum mechanics
- Relativity
- Relativity, General
- Relativity, Introduction to General
- Renormalization
- Renormalization group
- Representation theory
- Rietdijk-Putnam argument
- Shape dynamics
- Standard Model
- Standard Model (mathematical formulation)
- Statistical mechanics
- Stone-von Neumann theorem
- String theory
- Strong CP problem
- Supertask
- Supergravity
- Supersymmetry
- Thermal and statistical physics, Philosophy of
- Timeline of cosmological theories
- Timeline of particle physics
- Timeline of particle physics technology
- Timeline of quantum mechanics
- Topological order
- Ultraviolet catastrophe
- Universality
- Unruh effect
- Unsolved problems in physics, List of
- van der Waals, Johannes Diderik (1837-1923)
- Volta, Alessandro (1745-1827)
- von Neumann, John (1903-1957)
- Wave function
- Wave function collapse
- Wave-particle duality
- Weinberg-Witten theorem
- Weyl, Hermann (1885-1955)
- Wightman axioms
- Wigner, Eugene (1902-1995)
- Wigner’s classification
- Wigner’s theorem
- Wigner-Eckart theorem
7.17.5 Others
- bohmianmechanics.org
- Can the quantum state be interpreted statistically? - Matt Leifer
- Can we trivialize the equivalence between canonical quantization of fields and second quantization of particles? - physics.stackexchange
- Could one argue that \(h\) (Planck constant) and \(\hbar/2\) (Dirac constant) are in fact independant constants? - physics.stackexchange
- Clear Physics
- Effective field theory - nlab
- Emergence - RationalWiki.org
- Fiber bundles in physics - nlab
- Intuitively, why are bundles so important in Physics? - nlab
- Is a third quantization possible? - physics.stackexchange
- Kochen-Specker theorem
- lqp2.org - serving several papers on AQFT
- Philosophy of general relativity - Jonathan Bain
- Philosophy of quantum mechanics - Jonathan Bain
- Quantization - nLab
- What is a gauge? - Terence Tao
- Struggles With the Continuum - John Baez
- Kelvin’s “Clouds” Speech
7.17.6 Videos
- Al-Khalili, J. (2009). “Atom” BBC documentary (3 episodes)
- Carroll, S. (2013). Particles, Fields and The Future of Physics.
- Carroll, S. (2019). Something Deeply Hidden - talk at Google.
- Kuhn, R.L. (2020). Closer To Truth: What’s Strong Emergence?
- Maudlin, T. (2018). Ontological clarity, electromagnetism, Aharanov-Bohm effect.
- Tong, D. (2017). Quantum Fields: The Real Building Blocks of the Universe.