2 The scientific method
This outline discusses the history of science, the definition of the scientific method, its central role in founding a scientific epistemology, the demarcation of science from pseudoscience, and other epistemological topics concerning the methods and philosophy of science. The metaphysical implications of science are discussed in the Outline on scientific realism.
This could have been called the outline of “Epistemology”.
2.1 History of science
In this first section, we briefly outline chronologically highlights in the development of science, after which there are sections focusing on topics in the epistemology of science, starting with rationalism vs empiricism.
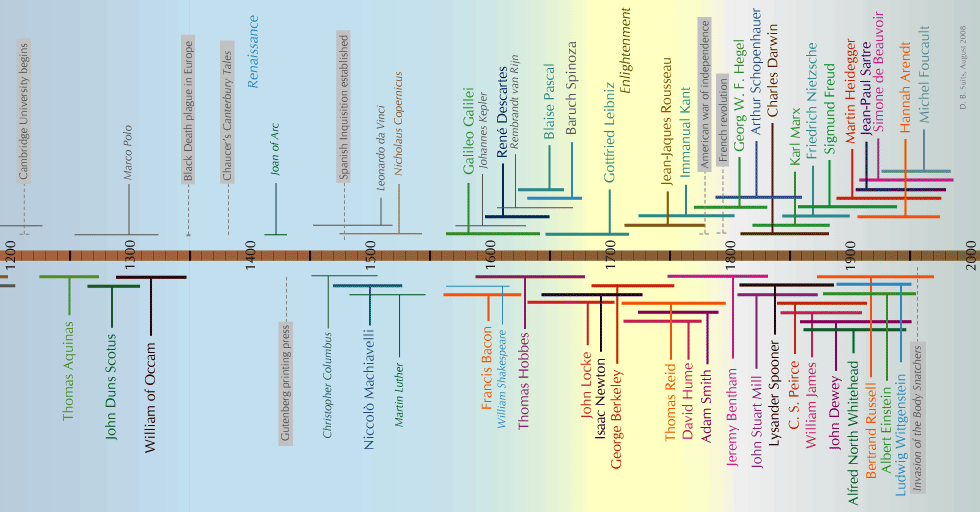
2.1.1 Antiquity
2.1.1.1 Eastern
- Kanada (c. 700-100 BCE)
- Mozi (470-391 BCE)
- skepticism, anti-dogmatism
- Zou Yan (305-240 BCE)
- Su Song (1020-1101)
- The Needham Question
See also:
2.1.1.2 Western
- Ionian Enlightenment
- “Ionian enchantment: A brief history of scientific naturalism” 1
- Thales of Miletus (c. 624/623-548/545 BCE)
- “first philosopher”
- predicted a solar eclipse in 585 BCE
- Anaximander (c. 610-546 BCE)
- Carlo Rovelli argues that Anaximander is the first scientist. 2
- speculated that humans evolved from fish?
- first to make a map?
- Anaximenes (c. 586-526 BCE)
- Xenophanes (c. 570-478 BCE)
- Pythagoras (570-495 BCE)
- radical mathematical realist
- Heraclitus (c. 535-475 BCE)
- Parmenides (b. c. 515 BCE)
- Anaxagoras (c. 510-428 BCE)
- first to suggest that the Sun is a star
- Zeno of Elea (c. 495-430 BCE)
- Empedocles (c. 494-434 BCE)
- theory of the four elements
- Protagoras (c. 490-420 BCE)
- major Sophist - professional tutor, especially in rhetoric.
- Herodotus (c. 484-425 BCE)
- “Father of history”
- Socrates (c. 470-399 BCE)
- First moral philosopher
- Socratic method
- Teacher of Plato and Xenophon
- Thucydides (c. 460-400 BCE)
- “Father of scientific history”
- Democritus (460-370 BCE)
- atomic theory
- Hippocrates (c. 460-370 BCE)
- “Father of medicine”
- Xenophon (c. 431-354 BCE)
- Plato (428/7 or 424/3 - 348/7 BCE)
- revolutionized western thought
- epistemology
- abstract Platonism
- Platonic Academy (387 BCE - 529 CE) from which we derive academia
- “the safest general characterization of the European philosophical tradition is that it consists of a series of footnotes to Plato.” 3
- Aristotle (384-322 BCE)
- His writings cover many subjects and have influenced the intellectual lexicon of virtually every field of study.
- Riddled with teleological explanation: things have “natural” purposes or tendencies.
- Founded the Lyceum (334-86 BCE)
- Tutored Alexander the Great ages 13-16 beginning in 343 BC.
- Prior Analytics (c. 350 BCE) - book that founded formal logic
- Peripatetic school
- Theophrastus (c. 371-287 BCE)
- Strato of Lampsacus (c. 335-269 BCE)
- Epicurus (341-270 BCE)
- Emphasized skepticism until something can be demonstrated
- Principle of Multiple Explanations: “if several theories are consistent with the observed data, retain them all”
- Zeno of Citium (c. 334-262 BCE)
- Euclid (fl. 300 BCE)
- logico-deductive method founded by Euclid’s Elements
- Aristarchus of Samos (310-230 BCE)
- first to posit heliocentrism
- Archimedes (c. 287-212 BCE)
- The Method
- Chrysippus (c. 279-206 BCE)
- Eratosthenes (276-195/194 BCE)
- Estimated the circumference of the Earth to be 50 times the distance between Alexandria and Syene, which was pretty acurate as it is actually 47.9 times! 4
- Library of Alexandria
- Library of Pergamum
- Apollonius of Perga (c. 240-190 BCE)
- Hipparchus (c. 190-120 BCE)
- Antikythera mechanism (between c. 200 and 100 BCE)
- Lucretius (99-55 BCE)
- Ptolemy (c. 100-170 CE)
- Almagest
- Diophantus (c. 200/214 - 284/298 CE)
Russell:
The Greeks contributed, it is true, something else which proved of more permanent value to abstract thought: they discovered mathematics and the art of deductive reasoning. Geometry, in particular, is a Greek invention, without which modern science would have been impossible. But in connection with mathematics the one-sidedness of the Greek genius appears: it reasoned deductively from what appeared self-evident, not inductively from what had been observed. Its amazing successes in the employment of this method misled not only the ancient world, but the greater part of the modern world also. It has only been very slowly that scientific method, which seeks to reach principles inductively from observations of particular facts, has replaced the Hellenic belief in deduction from luminous axioms derived from the mind of the philosopher. For this reason, apart from others, it is a mistake to treat the Greeks with superstitious reverence. Scientific method, though some few among them were the first men who had an inkling of it, is, on the whole, alien to their temper of mind, and the attempt to glorify them by belittling the intellectual progress of the last four centuries has a cramping effect upon modern thought.
There is however, a more general argument against reverence, whether for the Greeks or for anyone else. In studying a philosopher, the right attitude is neither reverence nor contempt, but first a kind of hypothetical sympathy, until it is possible to know what it feels like to believe in his theories, and only then a revival of the critical attitude, which should resemble, as far as possible, the state of mind of a person abandoning opinions which he has hitherto held. Contempt interferes with the first part of this process, and reverence with the second. 5
5 B. Russell (2004), p. 47.
Weinberg:
Like modern scientists, these early Greeks were willing to look beneath the surface appearance of the world, pursuing knowledge about a deeper level of reality. The matter of the world does not appear at first glance as if it is all made of water, or air, or earth, or fire, or all four together, or even atoms. 6
6 Weinberg (2015), p. 7.
Nevertheless, I think one should not overemphasize the modern aspects of Archaic or Greek science. There is an important feature of modern science that is almost completely missing in all the thinkers I have mentioned, from Thales to Plato: none of them attempted to verify or even (aside perhaps from Zeno) seriously to justify their speculations. In reading their writings, one continually wants to ask, “How do you know?” This is just as true of Democritus as of others. Nowhere in the fragments of his books that survive do we see any effort to show that matter really is composed of atoms. 7
7 Weinberg (2015), p. 11.
This did not occur to the early Greeks, or to many of their successors, for a very simple reason: they had never seen it done. 8
8 Weinberg (2015), p. 13.
- Review of To Explain the World 9
- Hoyningen-Huene, P. (2020). Beyond Kuhn and Feyerabend: After the fourth stage of philosophy of science.
- TODO: on removing Aristotle’s teleology from physics.
9 Davis (2015).
2.1.1.3 American
10 Keoke & Porterfield (2002).
2.1.1.4 African
See also:
2.1.2 The Middle Ages
- Islamic Golden Age
- Academy of Gondishapur
- in what is now Khuzestan Province, Iran
- House of Wisdom
- in Abbasid-era Baghdad, Iraq
- Muhammad ibn Musa al-Khwarizmi (c. 780-850)
- Ibn al-Haytham (965-1040) AKA “Alhazen”
- Book of Optics
- First to demonstrate the success of the intromission theory over the extramission theory of vision.
- Doubts Concerning Ptolemy
- “But for a man to imagine a circle in the heavens, and to imagine the planet moving in it does not bring about the planet’s motion… And therefore the arrangements assumed by Ptolemy for the five planets are false, and he asserted them knowing them to be false, and there exists for the planets a true arrangement in existing bodies which Ptolemy failed to grasp.” 11
- “Ibn al-Haytham was an early proponent of the concept that a hypothesis must be supported by experiments based on confirmable procedures or mathematical evidence—an early pioneer in the scientific method five centuries before Renaissance scientists.” - Wikipedia
- The first true scientist - By Jim Al-Khalili
- Ibn Sina (980-1037) AKA “Avicenna”
- Shen Kuo AKA Shen Gua (1031-1095)
- Reconquest of Toledo (1085)
- Scholasticism
- Robert Grosseteste (ca. 1168-1253)
- Roger Bacon (1214-1292)
- William of Ockham (1287-1347)
- Ockham’s razor as a hint at parsimony and abduction
11 Sabra (1978), p. 121–2.
2.1.3 Early Modern Period
- Renaissance
- Leonardo da Vinci (1452-1519)
- Nicolaus Copernicus (1473-1543)
- Tycho Brahe (1546-1601)
- Francis Bacon (1561-1626)
- Dyson quoting Francis Bacon
- Oxford Essential Quotations: Francis Bacon
- “God forbid that we should give out a dream of our own imagination for a pattern of the world.”
- The Great Instauration (1620) tr. J. Spedding
- “The subtlety of nature is greater many times over than the subtlety of the senses and understanding.”
- Novum Organum (1620) bk. 1, Aphorism 10 (tr. J. Spedding)
- “Read not to contradict and confute, nor to believe and take for granted, nor to find talk and discourse, but to weigh and consider.”
- Essays (1625) “Of Studies”
- Galileo Galilei (1564-1642)
- Johannes Kepler (1571-1630)
- Thomas Hobbes (1588-1679)
- Pierre Gassendi (1592-1655)
- René Descartes (1596-1650)
- Father of analytic geometry and modern philosophy
- No teleology. Matter plenum, vorticies.
2.1.4 The Age of Enlightenment
- The Age of Enlightenment
- Preliminary Discourse to the Encyclopedia of Diderot
- Robert Boyle (1627-1691)
- Isaac Barrow (1630-1677)
- John Locke (1632-1704)
- Baruch Spinoza (1632-1677)
- Robert Hooke (1635-1703)
- Isaac Newton (1642-1727)
- Gottfried Wilhelm Leibniz (1646-1716)
- Edmond Halley (1656-1742)
- William Jones (1675-1749)
- George Berkeley (1685-1753)
- Thomas Reid (1710-1796)
- David Hume (1711-1776)
- Denis Diderot (1713-1784)
- Jean le Rond d’Alembert (1717-1783)
- Immanuel Kant (1724-1804)
2.1.5 Canonical classical physics
- Benjamin Franklin (1706-1790)
- Leonhard Euler (1707-1783)
- Joseph-Louis Lagrange (1736-1813)
- Alessandro Volta (1745-1827)
- Pierre-Simon Laplace (1749-1827)
- André-Marie Ampère (1775-1836)
- Carl Friedrich Gauss (1777-1855)
- Siméon Denis Poisson (1781-1840)
- Joseph von Fraunhofer (1787-1826)
- Augustin-Louis Cauchy (1789-1857)
- Michael Faraday (1791-1867)
- Nicolas Léonard Sadi Carnot (1796-1832)
- Carl Gustav Jacob Jacobi (1804-1851)
- William Rowan Hamilton (1805-1865)
- William Thomson Kelvin (1824-1907)
- James Clerk Maxwell (1831-1879)
- Josiah Willard Gibbs (1839-1903)
- Ludwig Boltzmann (1844-1906)
2.1.6 “Scientists”
- Henry Cavendish (1731-1810)
- Antoine Lavoisier (1743-1794)
- Oxygen theory of combustion; overthrew phlogiston theory
- John Dalton (1766-1844)
- atomic theory
- Mary Somerville (1780-1872)
- On the Connexion of the Physical Sciences (1834)
- John Herschel (1792-1871)
- Preliminary Discourse (1831)
- William Whewell (1794-1866)
- Coined the term “scientist” (previously natural philosopher)
- John Stuart Mill (1806-1873)
- Louis Pasteur (1822-1895)
- Christine Ladd-Franklin (1847-1930)
- Discovery of Neptune (1846)
2.1.7 Biological evolution
- Erasmus Darwin (1731-1802)
- Charles Darwin (1809-1882)
- Gregor Mendel (1822-1884)
- Alfred Russel Wallace (1823-1913)
- Thomas Henry Huxley (1825-1895)
2.1.8 Modern physics
- Ernst Mach (1838-1916)
- Hendrik Lorentz (1853-1928)
- Henri Poincaré (1854-1912)
- Max Planck (1858-1947)
- David Hilbert (1862-1943)
- Marie Curie (1867-1934)
- Ernest Rutherford (1871-1937)
- Albert Einstein (1879-1955)
- Max Born (1882-1970)
- Niels Bohr (1885-1962)
- Edwin Schrödinger (1887-1961)
- Louis de Broglie (1892-1987)
- Wolfgang Pauli (1900-1958)
- Werner Heisenberg (1901-1976)
- Pascual Jordan (1902-1980)
- Paul Dirac (1902-1984)
- John von Neumann (1903-1957)
2.1.9 Modern statistics
- Charles Sanders Peirce (1839-1914)
- Karl Pearson (1857-1936)
- Ronald Fisher (1890-1962)
- Harold Jeffreys (1891-1989)
- Jerzy Neyman (1894-1981)
- Egon Pearson (1895-1980)
- John Tukey (1915-2000)
- C.R. Rao (1920-2023)
2.1.10 Computer science
- Charles Babbage (1791-1871)
- Ada Lovelace (1815-1852)
- George Boole (1815-1864)
- John von Neumann (1903-1957)
- Alonzo Church (1903-1995)
- Alan Turing (1912-1954)
- Konrad Zuse (1910-1995)
- ENIAC (1945)
- Herbert A. Simon (1916-2001)
- TODO
2.2 Rationalism vs empiricism
2.2.1 Introduction
- Early modern philosophy, coming out of medieval scholasticism
- Debates over the foundations of epistemology
- Skepticism
- a priori vs a posteriori
- Lead to the Age of Enlightenment
- Kant: “Answering the question: What is Enlightenment?”
- Sapere aude (“Dare to be wise”)
- Kant: “Answering the question: What is Enlightenment?”
- TODO: Rationalism and empiricism in Asia.
See also:
2.2.2 Early empiricists
Heraclitus:
The things that can be seen, heard, and learned are what I prize the most. 12
12 Heraclitus, Fragment 55.
- Francis Bacon (1561-1626)
- Galileo Galilei (1564-1642)
- Thomas Hobbes (1588-1679)
2.2.3 Rationalists
- René Descartes (1596-1650)
- Discourse on the Method (1637)
- “Je pense, donc je suis.”
- Meditations on First Philosophy (1641) 13
- “Ego sum, ego existo.”
- Principles of Philosophy (1644)
- “Ego cogito, ergo sum”
- Clear and distinct perceptions
- Descartes’ method
- Discourse on the Method (1637)
- Baruch Spinoza (1632-1677)
- Gottfried Wilhelm Leibniz (1646-1716)
- New Essays on Human Understanding (1765)
- Universal and necessary truths
- Leibniz’s influence on Kant
- Christian Wolff (1679-1754)
13 Descartes (2008).

2.2.4 British empiricists
- Robert Boyle (1627-1691)
- John Locke (1632-1704)
- Corpuscules
- An Essay Concerning Human Understanding (1689)
- Criticism of innate ideas
- Primary and secondary qualities
- Tabula rasa - “blank slate”
- George Berkeley (1685-1753)
- David Hume (1711-1776)
Hume:
[S]cepticism, when more moderate, may be understood in a very reasonable sense, and is a necessary preparative to the study of philosophy, by preserving a proper impartiality in our judgments, and weaning our mind from all those prejudices, which we may have imbibed from education or rash opinion. To begin with clear and self-evident principles, to advance by timorous and sure steps, to review frequently our conclusions, and examine accurately all their consequences; though by these means we shall make both a slow and a short progress in our systems; are the only methods, by which we can ever hope to reach truth, and attain a proper stability and certainty in our determinations. 16
16 Hume (2007), §XII, pp. 109–110.
2.2.5 Important synthesizers
- Isaac Newton (1642-1727)
- The Principia (1687) 17
- Immanuel Kant (1724-1804)
- Universal Natural History and Theory of the Heavens (1755)
- Nebular hypothesis of star and solar system formation
- Critique of Pure Reason (1781), 2nd edition in 1787 18
- Prolegomena to Any Future Metaphysics (1783)
- Metaphysical Foundations of Natural Science (1786)
- Critique of Practical Reason (1788)
- Critique of Judgment (1790)
- “It is absurd to hope that another Newton will arise in the future who will make comprehensible to us the production of a blade of grass according to natural laws”
- He was wrong!
- Universal Natural History and Theory of the Heavens (1755)
2.3 Knowledge
2.3.1 Definining knowledge
Plato:
19 Plato, Republic V 477–8, Cooper & Hutchinson (1997), p. 1103–4.
20 Plato, Theaetetus 186–7, Cooper & Hutchinson (1997), p. 205–7.
I myself do not have the answer when I perplex others, but I am more perplexed than anyone when I cause perplexity in others. So now I do not know what virtue is; perhaps you knew before you contacted me, but now you are certainly like one who does not know. Nevertheless, I want to examine and seek together with you what it may be. 21
21 Plato, Meno 80d, Cooper & Hutchinson (1997), p. 879.
- According to Plato, all knowledge is found through recollection.
- My tweet: Meno in a nutshell
- Fraser, Ed. (2012). Picking a fight with Plato.
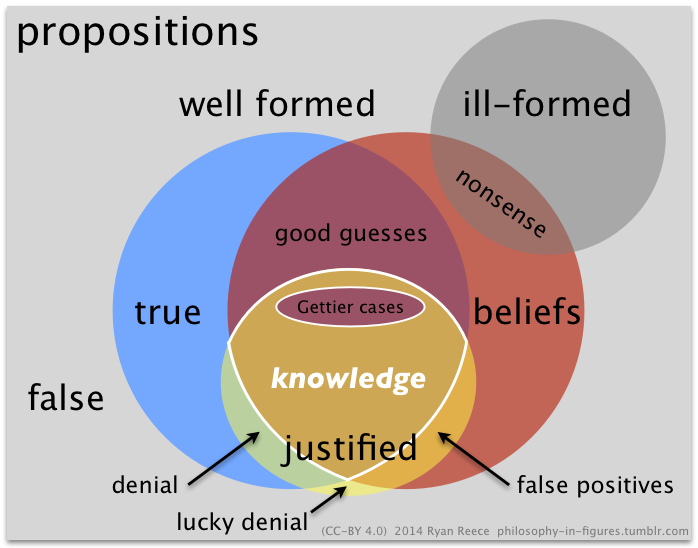
- Knowledge = Justified True Belief (JTB)
SOCRATES: Then suppose a jury has been justly persuaded of some matter which only an eye-witness could know, and which cannot otherwise be known; suppose they come to their decision upon hearsay, forming a true judgment: then they have decided the case without knowledge, but, granted they did their job well, being correctly persuaded?
THEAETETUS: Yes, certainly.
SOCRATES: But, my dear lad, they couldn’t have done that if true judgment is the same thing as knowledge; in that case the best juryman in the world couldn’t form a correct judgment without knowledge. So it seems they must be different things.
THEAETETUS: Oh, yes, Socrates, that’s just what I once heard a man say; I had forgotten, but now it’s coming back to me. He said that it is true judgment with an account that is knowledge; true judgment without an account falls outside of knowledge. And he said that the things of which there is no account are not knowable (yes, he actually called them that), while those which have an account are knowable.
SOCRATES: Very good indeed. 22
22 Plato, Theaetetus 201b–d, Cooper & Hutchinson (1997), p. 222–3.
In his unfinished work, Rules 23, Descartes defines “science” (scientia) in Rule 2 as
23 Descartes (1996), vol. 10, p. 362.
Omnis scientia est cognitio certa et evidens.
All (scientific) knowledge is certain and evident cognition.
In the same section, Descartes’ boldly declares to reject probable knowledge for only what is perfectly certain:
we reject all […] merely probable cognition and resolve to believe only what is perfectly known and incapable of being doubted.
- Chisholm, R. (1966). Theory of Knowledge. 24
- The Problem of Criterion
- Nozick, R. (1981). Philosophical Explanations. 25
Ichikawa & Jenkins:
The standard analysis of knowledge says that for any subject \(S\) and any proposition \(p\), the following are individually necessary and jointly sufficient conditions for \(S\) knows that \(p\):
- \(p\)
- \(S\) believes that \(p\)
- \(S\) is justified in believing that \(p\).
Precursors of this view are sometimes attributed to Plato, who says in the Meno that knowledge is distinguished from mere true belief in being ‘tied down’, so that it cannot easily escape or be lost as mere true belief can. Views more closely resembling the above formulation of the JTB analysis are attributed by Edmund Gettier to Roderick Chisholm and A. J. Ayer. Neither of those authors phrased their conditions for knowledge exactly this way. The now-usual formulation, in terms of justification, is so in large part because of Gettier (1963). 26
26 Ichikawa & Jenkins (2017).
2.3.2 Epistemic errors
2.3.2.1 Fallibility
- Fallibility
Sophocles:
One must learn by doing the thing; though you think you know it, you have no certainty until you try.
Feynman:
All scientific knowledge is uncertain… [W]hat we call scientific knowledge today is a body of statements of varying degrees of certainty. Some of them are most unsure. Some of them nearly sure; but none of them is certain. 27
27 Feynman (1998), p. 26–27.
The stopped clock from Russell’s Human Knowledge: Its Scope and Limits. Russell:
You’re walking by a clock that you’ve always known to be accurate in the past. You glance up at it and see that it reads five o’clock; on the basis of this you believe that it’s five o’clock. Your belief is justified, and as it happens it is five o’clock. But unbeknownst to you, the clock stopped exactly twelve hours ago. 28
28 B. Russell (2009).
2.3.2.2 Gettier cases
2.3.2.3 Systematic uncertainties
- Failed justification
- Mayo on error statistics and severe testing
- TODO: discussion by me
See also:
2.3.2.4 Internalism vs externalism
- TODO?
2.3.3 Scientific knowledge
- Aristotle: scientific knowledge is to “know the cause on which the fact depends”
- Scientific method, community, and body of knowledge
- Naturalism
- Hume on the problem of induction and the uniformity of nature, again
- Monism
- Reductionism
- Ontological implications of science
- Positivism
- Realism
- Big data
- Martínez-Ordaz, M. del R. (2021). Is there anything special about the ignorance involved in big data practices? 31
- Criticism: scientism
- Are there other ways of knowing?
- Zero-knowledge proof
- Proof of knowledge (cryptography)
- Silvio Micali: Lex Fridman podcast - 1h25+
- Verification and knowledge are different concepts
- Mallick, C. (2022). Understanding zero knowledge proof.
- Chitra, T. & Prior, H. (2023). Do language models possess knowledge (soundness)?
31 Martínez-Ordaz (2021).
From Aristotle’s Posterior Analytics:
We suppose ourselves to possess unqualified scientific knowledge of a thing, as opposed to knowing it in the accidental way in which the sophist knows, when we think that we know the cause on which the fact depends, as the cause of that fact and of no other, and, further, that the fact could not be other than it is. 32
32 Aristotle (2007), book 1, chapter 2.
another translation:
We think we understand something simpliciter (and not in the sophistical way, incidentally) when we think we know of the explanation because of which the object holds that it is its explanation, and also that it is not possible for it to be otherwise. It is plain, then, that to understand is something of this sort. 33
33 Aristotle (1993), book 1, chapter 2.
See also:
- Sean Carroll on scientific epistemology: debate with Hans Halvorson
- Outline on scientific realism
- Outline on naturalism
2.4 Analytic/synthetic distinction
2.4.1 Introduction
- Locke
- An Essay Concerning Human Understanding (1689)
- Hume’s fork
- Relations of ideas vs matters of fact
- Dicker, G. (1991). Hume’s fork revisited. 34
34 Dicker (1991).
Hume:
When we run over libraries, persuaded of these principles, what havoc must we make? If we take in our hand any volume; of divinity or school metaphysics, for instance; let us ask, Does it contain any abstract reasoning concerning quantity or number? No. Does it contain any experimental reasoning concerning matter of fact and existence? No. Commit it then to the flames: for it can contain nothing but sophistry and illusion. 35
35 Hume (2007), §XII, p. 120.
| analytic | synthetic | |
|---|---|---|
| a priori | True by definition Hume’s relations of ideas |
Kant: Arithmetic propositions? Kant: Transcendental deduction? |
| a posteriori | Impossible? | Empirical Hume’s matters of fact |
- Kant
- Critique of Pure Reason (1781)
- Are there synthetic a priori statements? Kant thinks so.
- Kant argues that all of pure mathematics is synthetic a priori, even in the simple example “7 + 5 = 12”, since the concept of “12” is not contained in the concepts of “7”, “5”, or “+”. 36
- Transcendental Deduction of the Categories (TDC): An argument that aims to justify the use of a concept, one that demonstrates that the concept correctly applies to objects of experience.
- “No analysis without prior synthesis”
- Twitter thread on the CPR by Helen De Cruz - (threadreadered)
36 Kant (1996), p. B15–16.
Kant in his Critique of Pure Reason (1787):
In all judgments in which we think the relation of a subject to the predicate… this relation is possible in two ways. Either the predicate B belongs to the subject A as something that is (covertly) contained in this concept A; or B, though connected with concept A, lies quite outside it. In the first case I call the judgment analytic; in the second, synthetic. Hence (affirmative) analytic judgments are those in which the predicate’s connection with the subject is thought by [thinking] identity, whereas those judgments in which this connection is thought without [thinking] identity are to be called synthetic. Analytic judgments could also be called elucidatory. For they do not through the predicate add anything to the concept of the subject; rather, they only dissect the concept, breaking it up into its component concepts which had already been thought in it (although thought confusedly). Synthetic judgments, on the other hand, could also be called expansive. For they do add to the concept of the subject a predicate that had not been thought in that concept at all and could not have been extracted from it by any dissection. 37
37 Kant (1996), p. A6–7, B10–11.
and
logic is a science that provides nothing but a comprehensive exposition. 38
38 Kant (1996), p. Bviii–ix.
and
Now the proper problem of pure reason is contained in this question:
How are synthetic judgments possible a priori? 39
39 Kant (1996), p. B19.
Moore:
It is a well-known fact in the history of philosophy that necessary truths in general, but especially those of which it is said that the opposite is inconceivable, have been commonly supposed to be analytic, in the sense that the proposition denying them was self-contradictory. It was in this way, commonly supposed, before Kant, that many truths could be proved by the law of contradiction alone. 40
40 Moore (1903), p. 6–7.
Vienna Circle manifesto:
In such a way logical analysis overcomes not only metaphysics in the proper, classical sense of the word, especially scholastic metaphysics and that of the systems of German idealism, but also the hidden metaphysics of Kantian and modern apriorism. The scientific world-conception knows no unconditionally valid knowledge derived from pure reason, no ‘synthetic judgments a priori’ of the kind that lie at the basis of Kantian epistemology and even more of all pre- and post-Kantian ontology and metaphysics. The judgments of arithmetic, geometry, and certain fundamental principles of physics, that Kant took as examples of a priori knowledge will be discussed later. It is precisely in the rejection of the possibility of synthetic knowledge a priori that the basic thesis of modern empiricism lies. The scientific world-conception knows only empirical statements about things of all kinds, and analytic statements of logic and mathematics. 41
41 Hahn, Neurath, & Carnap (1973), §2.
See also:
2.4.2 Formal epistemology
- Formal epistemology
- Hendricks, V.F. (2006). Mainstream and Formal Epistemology. 42
- Hansson, S.O. & Hendricks, V.F. (2018). Introduction to Formal Philosophy. 43
- Pettigrew, R. & Weisberg, J. (2019). The Open Handbook of Formal Epistemology. 44
Carnap:
- In The Logical Syntax of Language (LSL),
analytic: \(L\)-valid,
contradictory: \(L\)-contravalid,
synthetic: \(L\)-indeterminate. 45 - Carnap rejects the synthetic a priori:
45 Carnap (1937), p. 182.
Theorem 52.3. Every logical sentence is \(L\)-determinate; there are no synthetic logical sentences. 46
46 Carnap (1937), p. 184.
Theorem 60c.1. If \(S\) is consistent, or at least non-contradictory, then ‘analytic (in \(S\))’ is indefinable in \(S\). 47
47 Carnap (1937), p. 219.
- Carnap, R. (1950). Empiricism, semantics, and ontology. 48
- Internal vs external questions
- Awodey, S. & Carus, A.W. (2007). Carnap’s dream: Gödel, Wittgenstein, and Logical Syntax. 49
Kripke:
- Claims there are a posteriori necessary truths in Naming and Necessity (1972). 50
50 Kripke (1980).
Papineau:
- Philosophical Devices (2012) 51
51 Papineau (2012).
See also:
2.4.3 Criticisms
Einstein:
As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality. 52
52 Einstein (1922), p. TODO.
and
I am even of the opinion that this standpoint [Kant’s system of a priori concepts and norms] cannot be strictly refuted by any scientific development. For, one will always be able to say that critical philosophers had hitherto erred in setting up the a priori elements and one will always be able to set up a system of a priori elements that does not conflict with a given physical system. I surely may briefly indicate why I do not find this standpoint natural. Let a physical theory consist of the parts (elements) \(A\), \(B\), \(C\), \(D\), which together form a logical whole that correctly connects the pertinent experiments (sensory experiences). Then the tendency is that less than all four elements, e.g., \(A\), \(B\), \(D\), still say nothing about the experiences, without \(C\); no more so \(A\), \(B\), \(C\), without \(D\). One is then free to regard three of these elements, e.g., \(A\), \(B\), \(C\), as a priori and only \(D\) as empirically determined. What always remains unsatisfactory in this is the arbitrariness of the choice of elements to be designated as a priori, even disregarding that the theory could be replaced at some point by another theory that substitutes some of these elements (or all four of them) with others. One could be of the view, though, that through direct analysis of human reason, or thought, we would be in a position to recognize elements that would have to be present in any theory. But most researchers would probably agree that we lack a method for recognizing such elements, even if one were inclined to believe in their existence. Or should one imagine that the search for a priori elements was a kind of asymptotic process that advances along with the development of science? 53
53 Norton (2017).
- Norton, J.D. (2017). Einstein on Kant.
- Quine, W.V.O. (1951). Two dogmas of empiricism. 54
- Quine, W.V.O. & Carnap, R. (1990). Dear Carnap, Dear Van: The Quine-Carnap Correspondence and Related Work. 55
See also:
- Longer discussion of the Attack on the analytic/synthetic distinction in the section on Postpositivism.
2.4.4 Discussion
- Stearns, P. (2020). Epistemology: A priori vs. a posteriori, analytic vs. synthetic, necessary vs. contingent.
- relationship to necessity and contingency
- Kripke
- Hintikka
- Russell, G. (2008). Truth in Virtue of Meaning: A defence of the analytic/synthetic distinction. 56
- Juhl, C. & Loomis, E. (2009). Analyticity. 57
- Weatherson, B. (2017). Analytic-synthetic and a priori-a posteriori. 58
- de Swart, H. (2018). Philosophical and Mathematical Logic. 59
- TODO: How much of this should be moved to the longer discussion of the Attack on the analytic/synthetic distinction in the section on Postpositivism?
de Swart:
Sometimes one speaks of logically necessary truths instead of analytic truths and of logically contingent truths instead of synthetic truths, to be distinguished from physically necessary truths (truths which physically could not be otherwise, true in all physically possible worlds). The distinction between necessary and contingent truth is a metaphysical one, to be distinguished from the epistemological distinction between a priori and a posteriori truths. Although these—the metaphysical and the epistemological—are certainly different distinctions, it was controversial whether they coincide in extension, that is, whether all and only necessary truths are a priori and all and only contingent truths are a posteriori. 60
60 de Swart (2018), p. 141–2.
Gillian Russell:
[O]ur old view of analyticity was based on a naive theory of meaning, and some Quinean challenges to it were basically right. But our new theories of meaning will support a new picture of analyticity, one which—being based on a better theory of meaning—admits of a more robust defence. 61
61 G. Russell (2008), p. xi.
2.5 Induction
2.5.1 Problem of induction
- How do we infer universals from particulars?
- Past performance is no guarantee of future results.
- Fallacy: hasty generalization
- Ex ante probability
- Note that philosophical induction is not mathematical induction.
Sextus Empiricus:
When they propose to establish the universal from the particulars by means of induction, they will effect this by a review of either all or some of the particulars. But if they review some, the induction will be insecure, since some of the particulars omitted in the induction may contravene the universal; while if they are to review all, they will be toiling at the impossible, since the particulars are infinite and indefinite. 62
62 Sextus Empiricus (1933), p. 283.
Leibniz:
The senses, although they are necessary for all our actual knowledge, are not sufficient to give us the whole of it, since the senses never give anything but instances, that is to say particular or individual truths. Now all the instances which confirm a general truth, however numerous they may be, are not sufficient to establish the universal necessity of this same truth, for it does not follow that what happened before will happen in the same way again… And any one who believed that [day must follow night] is a necessary and eternal truth which will last for ever, would likewise be wrong, since we must hold that the earth and even the sun do not exist of necessity, and that there may perhaps come a time when that beautiful star and its whole system will exist no longer, at least in its present form. From which it appears that necessary truths, such as we find in pure mathematics, and particularly in arithmetic and geometry, must have principles whose proof does not depend on instances, nor consequently on the testimony of the senses, although without the senses it would never have occurred to us to think of them. 63
63 Leibniz (1996), p. TODO.
Hume:
Locke divides all arguments into demonstrative and probable. In this view, we must say, that it is only probable that all men must die, or that the sun will rise tomorrow. But to conform our language more to common use, we ought to divide arguments into demonstrations, proofs, and probabilities—by proofs meaning such arguments from experience as leave no room for doubt or opposition. 64
64 First footnote in the essay “On Probability” in Hume (2007), p. 56.
- Chārvāka - ancient Indian philosophy
- Hume
- Russell’s inductive turkey
- TODO: find Russell ref
- Note discussion by French
- Ayer
- Psillos, S. (2020). The problem of induction. IEP.
Dewey:
2.5.2 Causation
Hume:
Even after the observation of the frequent conjunction of objects, we have no reason to draw any inference concerning any object beyond those of which we have had experience.
– David Hume, in A Treatise of Human Nature, Book I, part 3, §12.
- Bertrand Russell
- Nancy Cartwright
- Judea Pearl
- James Woodward
See also:
2.5.3 Uniformity of nature
- Hume on the uniformity of nature
- Uniformitarianism
- Lyell, Charles. (1830). Principles of Geology.
- Mill on the uniformity of nature
- Salmon, W.C. (1953). The uniformity of nature. 68
- Gould, S. J. (1965). Is uniformitarianism necessary? 69
- TODO: contemporary view
- TODO: Science requires some uniformity of nature, e.g. astronomy, but such uniformity is also empirically confirmed.
- Unless we have a collective and/or non-local conspiracies, we can probablistically justify assumptions of uniformity.
See also:
2.5.4 Inductive logic
Newton:
In experimental philosophy, propositions gathered from phenomena by induction should be considered exactly or very nearly true not withstanding any contrary hypothesis, until yet other phenomena make such propositions either more exact or liable to exceptions. 70
70 Newton (2016), p. TODO.
- Thomas Bayes (1701-1761)
- Richard Price (1723-1791)
- Pierre-Simon Laplace (1749-1827)
- William Whewell (1794-1866)
- Philosophy of the Inductive Sciences (1840)
- Discussed in Aronson 71
- John Stuart Mill (1806-1873)
- A System of Logic (1843) 72
- Charles S. Peirce (1839-1914)
Price knew the work of Bayes well. Concerning Bayes’ “An Essay towards Solving a Problem in the Doctrine of Chances” (1763),
It was on this essay, and on an Appendix which Price himself authored, that Price drew in fashioning his critique of Hume’s “Of Miracles”. In Four Dissertations, Price gives a reference to Bayes’ paper. But it is doubtful that Hume read the paper, and even if he had it is even more doubtful that Hume would have understood it because he was unfamiliar with the technical developments in the probability calculus.
Is it then fair to use this apparatus as part of a critique of Hume’s argument against miracles? My answer is an unqualified yes. In the Abstract to the Treatise, Hume endorses Leibniz’s complaint that various authors, including Locke, are “too concise when they treat of probabilities, and those other measures of evidence on which life and action intirely depend, and which are our guides even in most of our philosophical speculations.” The Abstract announces that “The author of the treatise of human nature seems to have been sensible of this defect in these philosophers, and has endeavoured, as much as he can, to supply it” (T 647). Of course, by “probabilities” Hume did not have in mind reasoning that proceeds by proving and applying theorems of the probability calculus. But ignorance of the apparatus is no excuse since, for example, before the end of the seventeenth century, there were published attempts to apply the probability calculus to some of the questions at issue in Hume’s essay, such as the effect of multiple witnesses. A number of Hume’s contemporaries, such as Price, understood Hume’s claims as being about quantifiable degrees of belief or credibility, the quantification being subject to the constraints of the probability calculus. 73
73 Earman (2000), p. 25.
Vickers:
[I]n Peirce’s phrase, inductions are ampliative. Induction can amplify and generalize our experience, broaden and deepen our empirical knowledge. Deduction on the other hand is explicative. Deduction orders and rearranges our knowledge without adding to its content. 74
74 Vickers (2014) (emphasis added).
Peirce on merely the denial of any major failures of induction and the wonderful self-correcting nature of ampliative inference:
Peirce:
I maintain that it has been shown that the modes of inference in question are necessarily valid, whatever the constitution of the universe, so long as it admits of the premises being true. Yet I am willing to concede, in order to concede as much as possible, that when a man draws instances at random, all that he knows is that he tries to follow a certain precept; so that the sampling process might be rendered generally fallacious by the existence of a mysterious and malign connection between the mind and the universe, such that the possession by an object of an unperceived character might influence the will toward choosing it or rejecting it. Such a circumstance would, however, be as fatal to deductive as to ampliative inference. Suppose, for example, that I were to enter a great hall where people were playing rouge et noir at many tables; and suppose that I knew that the red and black were turned up with equal frequency. Then, if I were to make a large number of mental bets with myself, at this table and at that, I might, by statistical deduction, expect to win about half of them, —precisely as I might expect, from the results of these samples, to infer by induction the probable ratio of frequency of the turnings of red and black in the long run, if I did not know it. But could some devil look at each card before it was turned, and then influence me mentally to bet upon it or to refrain therefrom, the observed ratio in the cases upon which I had bet might be quite different from the observed ratio in those cases upon which I had not bet. I grant, then, that even upon my theory some fact has to be supposed to make induction and hypothesis valid processes; namely, it is supposed that the supernal powers withhold their hands and let me alone, and that no mysterious uniformity or adaptation interferes with the action of chance. But then this negative fact supposed by my theory plays a totally different part from the facts supposed to be requisite by the logicians of whom I have been speaking. So far as facts like those they suppose can have any bearing, they serve as major premises from which the fact inferred by induction or hypothesis might be deduced; while the negative fact supposed by me is merely the denial of any major premise from which the falsity of the inductive or hypothetic conclusion could in general be deduced. Nor is it necessary to deny altogether the existence of mysterious influences adverse to the validity of the inductive and hypothetic processes. So long as their influence were not too over whelming, the wonderful self-correcting nature of the ampliative inference would enable us, even if they did exist, to detect and make allowance for them. 75
75 Peirce (1883), p. 176–7.
- Carnap
- “On inductive logic” 76
- Logical Foundations of Probability 77
- The Continuum of Inductive Methods 78
- “The aim of inductive logic” 79
- “Notes on probability and induction” 80
- French, C.F. (2015). Philosophy as Conceptual Engineering: Inductive Logic in Rudolf Carnap’s Scientific Philosophy. 81
- Chalmers, D.J. (2020). What is conceptual engineering and what should it be?. 82
- Isaac, M.G. & Koch, S. (2022). Foundational issues in conceptual engineering: Introduction and overview. 83
- Reichenbach
- Cross induction
- TODO: Reichenbach 84
76 Carnap (1945).
77 Carnap (1950b).
78 Carnap (1952).
79 Carnap (1966).
80 Carnap (1973).
81 C. F. French (2015).
82 Chalmers (2020).
83 Isaac & Koch (2022).
Reichenbach:
It will appear plausible that this answer was given in the frame of a theory of probability, though the form of this theory is very different from what might be expected. To say that observations of the past are certain, whereas predictions are merely probable, is not the ultimate answer to the question of induction; it is only a sort of intermediate answer, which is incomplete unless a theory of probability is developed that explains what we should mean by “probable” and on what ground we can assert probabilities. 85
85 Reichenbach (1968), p. 93-4.
- Russell
- Bayesian updating
- See also: Bayes’ theorem
- Aumann’s agreement theorem
- Aumann, R.J. (1976). Agreeing to disagree. 86
- Geanakoplos, J.D. & Polemarchakis, H.M. (1982). We can’t disagree forever. 87
- Aaronson, S. (2005). The complexity of agreement. 88
- Popper-Miller theorem
- Popper, K. & Miller, D. (1983). A proof of the impossibility of inductive probability. 89
- Eells, E. (1988). On the alleged impossibility of inductive probability. 90
- Sankey, H. (2008). Scientific Realism and the Rationality of Science. 91
- Vickers, J.M. (2013). Oxford Bibliography on Inductive Reasoning.
86 Aumann (1976).
87 Geanakoplos & Polemarchakis (1982).
88 Aaronson (2005).
89 K. Popper & Miller (1983).
90 Eells (1988).
91 Sankey (2008), p. 79.
See also:
2.5.5 Challenges
- Goodman: New riddle of induction (grue)
- Hempel: Raven paradox
- Putnam
- Van Fraassen
See also:
2.5.6 Abduction
- Peirce
- Douven, I. (2011). Abduction. SEP. 92
- Ockham, parsimony
- Karl Popper
- Inference to the best explanation
- Quine: Natural kinds, abstraction
- Bhaskar
- Convergence
92 Douven (2011).
Wikipedia:
Bhaskar also offers a practical solution to the problem. He argues that the problem of induction only arises if we deny the possibility of a reason for the predicate, located in the enduring nature of something. For example, we know that all emeralds are green, not because we have only ever seen green emeralds, but because the chemical make-up of emeralds insists that they must be green. If we were to change that structure, they would not be green. For instance, emeralds are a kind of green beryl, made green by trace amounts of chromium and sometimes vanadium. Without these trace elements, the gems would be colourless. 93
93 Bhaskar (2008).
Wikipedia:
Today abduction remains most commonly understood as induction from characters and extension of a known rule to cover unexplained circumstances. 94
Peirce:
The surprising fact, C, is observed;
But if A were true, C would be a matter of course,
Hence, there is reason to suspect that A is true. 95
95 Ibid.
Schurz:
General schema of abduction (or inference to the best explanation, IBE)
Premise 1: A (singular or general) fact E, in need of explanation.
Premise 2: Background knowledge K, which implies for some hypothesis H that H is a sufficiently plausible explanation for E.
—
Abductive conjecture: H is true. 96
96 Schurz (2019), p. 3.
Arthur Conan Doyle:
[W]hen you have eliminated the impossible, whatever remains, however improbable, must be the truth. 97
97 Doyle (1890), ch. 6.
See also:
2.5.7 Statistics as a solution to the problem of induction
- Reichenbach 98
- Weisberg 99 - nope
- Salmon 100
- Good 101
- Howson 102
- Hacking 103
- Huber 104
- Rao, C.R. (1997). Statisitcs and Truth: Putting Chance to Work. 105
98 TODO: Find Reichenbach references; could use previous ones.
99 Weisberg (2019), Appendix D.
100 Salmon (1963), Salmon (1966), Salmon (1967), Salmon (1991). TODO: Break up and go through these references.
101 Good (1988).
102 thebsps.org/auxhyp/howson/. TODO: Go through the Howson articles.
103 Hacking (2001).
104 Huber (2007).
105 Rao (1997).
See also:
- Outline of philosophy of statistics
- Note the further discussion of Humeanism and laws of nature in the Outline on scientific realism.
2.5.8 Meta-induction as a solution to the problem of induction
- Earnshaw, E. (2017). How I solved Hume’s problem and why nobody will believe me. 106
- Schurz, G. (2019). Hume’s Problem Solved: The optimality of meta-induction. 107
2.6 Is there a universal scientific method?
2.6.1 First pass
Feynman:
[S]cience is a method of finding things out. This method is based on the principle that observation is the judge of whether something is so or not. All other aspects and characteristics of science can be understood directly when we understand that observation is the ultimate and final judge of the truth of an idea… That is the principle of science. If there is an exception to any rule, and it can be proved by observation, that rule is wrong. 108
108 Feynman (1998), p. 15–16.
Feynman:
There are in science a number of technical consequences that follow from the principle of observation as judge. For example, the observation cannot be rough. You have to be very careful. There may have been a piece of dirt in the apparatus that made the color change; it was not what you thought. You have to check the observations very carefully, and then recheck them, to be sure that you understand what all the conditions are and that you did not misinterpret what you did. 109
109 Feynman (1998), p. 17.
- TODO: model of science taught in high schools—form a hypothesis, etc.
Sagan:
Spin more than one hypothesis, think of all the different ways in which it could be explained. Then think of tests by which you might systematically disprove each of the alternatives. What survives, the hypothesis that resists disproof in this Darwinian selection among ‘multiple working hypotheses’, has a much better chance of being the right answer than if you had simply run with the first idea that caught your fancy. 110
110 Sagan (1997), p. 197.
2.6.2 Yes: Models of science
- Robert Grosseteste (ca. 1168-1253)
Wikipedia:
Grosseteste was the first of the Scholastics to fully understand Aristotle’s vision of the dual path of scientific reasoning: generalising from particular observations into a universal law, and then back again from universal laws to prediction of particulars. Grosseteste called this “resolution and composition”. So, for example, looking at the particulars of the moon, it is possible to arrive at universal laws about nature. Conversely once these universal laws are understood, it is possible to make predictions and observations about other objects besides the moon. Grosseteste said further that both paths should be verified through experimentation to verify the principles involved.
- Hypothetico-deductive model
- Positivism, verificationism
- Auguste Comte, Ernst Mach, David Hilbert, Rudolf Carnap
- Logical empiricism
- Deductive-nomological model
- Falsification, deductivism
- Karl Popper
- The Logic of Scientific Discovery 115
- Pragmatic model
- C.S. Peirce
- Nola & Sankey 116
- Normal vs revolutionary science
- Thomas Kuhn
- The Structure of Scientific Revolutions 117
- Paradigm shifts
- Lakatos: Scientific Research Programs (SRPs)
- Laudan: normative naturalism.
- Distinction between exploratory data analysis and confirmatory data analysis
- Bayesian methodology
- Thomas Bayes, Pierre-Simon Laplace, Harold Jeffreys
- Error-catching filters
- Communist norm
- Heesen, R. (2017). Communism and the incentive to share in science. 120
- Bright, L.K. & Heesen, R. (2023). To be scientific is to be communist. 121
111 S. French (2007), p. TODO.
112 Nola & Sankey (2007), p. TODO.
113 Hempel & Oppenheim (1948).
114 S. French (2007), p. TODO.
115 K. R. Popper (2002).
116 Nola & Sankey (2007), p. TODO.
117 Kuhn (1962).
118 Ladyman, Ross, Spurrett, & Collier (2007).
119 Mayo & Spanos (2011).
120 Heesen (2017).
121 Bright & Heesen (2023).
Kant:
Whether someone’s treatment of the cognitions pertaining to reason’s business does or does not follow the secure path of a science—this we can soon judge from the result. If, after many preparations and arrangements have been made, the treatment falters as soon as it turns to its purpose; or if, in order to reach that purpose, it repeatedly has to retrace its steps and enter upon a different path; or, again, if the various collaborators cannot be brought to agree on the manner in which their common aim is to be achieved—then we may rest assured that such an endeavor is still far from having entered upon the secure path of a science, but is a mere groping about. We shall indeed be rendering a service to reason if we can possibly discover that path, even if we should have to give up as futile much that was included in the purpose which we had previously adopted without deliberation. 122
122 Kant (1996), p. B vii.
- Spivak, D.I. (2013). Category theory for scientists. 123
- In the introduction, in a rather positivist way, Spivak describes his view that category theory can be used to ground truth in observation.
123 Spivak (2013).
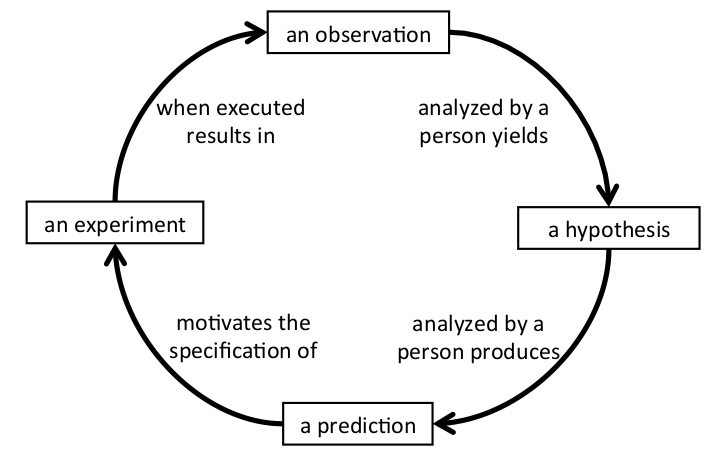
124 Spivak (2013), p. 5.
See also:
2.6.3 No: There is no unified “scientific method”
- Kuhn
- Paradigm shifts as a kind of pessimism
- Incommensurability: the language and theories of different paradigms cannot be translated into one another or rationally evaluated against one another.
- Feyerabend
- “Anything goes”
- Against Method 125
- McComas
- Allain
- “What’s wrong with the scientific method?” 129
- Blachowicz
2.6.4 Yes: Rebuttals in favor of scientific method
- Kuhn
- Later Kuhn is more nuanced. 132
- Feyerabend
- Like Kuhn, later Feyerabend is more nuanced.
- Nola and Sankey argue that in later writings Feyerabend backtracked. 133
- Not a seven-step program
- Evidence based, anti-conspiracy, parsimony
- Madsen, M.E. (2017). The real core of the scientific method and why we should trust it.
- Nola, R. (1999). On the possibility of a scientific theory of scientific method. 134
- Nola, R. & Sankey, H. (2007). Theories of Scientific Method. 135
- Hintikka
- Hintikka, J. (1999). Inquiry as Inquiry: A logic of scientific discovery. 136
- Schurz
- New foundationalist epistemology 137
- See also: No free lunch theorems
- Scientism
- Scientism: Scientific methods and meta-methods are universally applicable (in principle).
- See the Outline on naturalism
2.6.5 Anthropology of science
- Sociology of Scientific Knowledge (SSK)
- Strong programme
- David Bloor (b. 1942)
- Marks, J.M. (2009). Why I Am Not A Scientist: Anthropology and Modern Science. 138
- Reviewed by Wolf-Meyer, M.
138 Marks (2009).
2.7 Models in science
- TODO1: priority section to finish
2.7.1 What’s a model?
French:
[S]cientist don’t simply deduce experimental/observational consequences; they construct models that ‘mediate’ between theories and the observations. There are a number of reasons why scientists will proceed in this way but one is that theories are often quite complex and difficult to work with. So a scientist may build a simplified model, containing significant idealizations that allow the scientist to ignore certain factors, for example, and [more] easily relate the theory to observations. 139
139 S. French (2007), p. 81.
Holm:
Fermat’s principle (that the light ray passing from one point to another in an optical medium takes the path of stationary optical length) is complementary to Huygens’ principle (that a later wave front emerges as the envelope of wavelets emitted from the present wave front). Both principles are only models of reality, but they are models in the best sense. Both are transcendent fabrications that intuited the results of a later, more fundamental principle (Maxwell’s equations) and gave accurate predictions at the level of physical perception in their time. Without being the full truth by being physically tenable themselves, they fulfilled the tasks for which they were developed and they laid the foundations for more fundamental theories. Light rays do not exist and points along a light wave do not emit light. However, both principles work quite well in the design of optical instruments! In addition, both principles are still interesting now as the mathematical definitions of rays and wave fronts, respectively, although neither fully represents the physical principles of optics. 140
140 Holm (2011), p. xvi.
Model the theory:
\[ \text{Theory} + \text{Modeling} \longrightarrow \text{Model} \]
Fit the model to the data to make inferences on the theory:
\[ \text{Model} + \text{Data} + \text{Statistical Analysis} \longrightarrow \text{Model(improved)} \longrightarrow \text{Theory(improved)} \]
2.7.2 Models represent theories
Model the theory:
\[ T(\theta_k, \psi_m) \longrightarrow M(X_i | \theta_k, \nu_\ell) \]
Fit the model to the data to make inferences on the theory:
\[ \{X_i\}_j \longrightarrow M(X_{ij} | \theta_k, \nu_\ell) \longrightarrow \hat{\theta}_k \pm \sigma_{\hat{\theta}_k} , \hat{\nu}_\ell \pm \sigma_{\hat{\nu}_\ell} \longrightarrow T(\hat{\theta}_k \pm \sigma_{\hat{\theta}_k}, \psi_m) \]
Cox:
The very word model implies idealization of the real system and, except just possibly in the more esoteric parts of modern physics … it hardly makes sense to talk of a model being true. 141
141 Cox (2006), p. 84.
Frigg:
Morgan and Morrison (1999) rally around the idea that models are instruments that mediate between theories and the world. Models are “autonomous agents” in that they are independent from both theories and their target systems, and it is this independence that allows them to mediate between the two. Theories do not provide us with algorithms for the construction of a model; they are not “vending machines” into which one can insert a problem and a model pops out (Cartwright 1999). The construction of a model often requires detailed knowledge about materials, approximation schemes, and the setup, and these are not provided by the corresponding theory. Furthermore, the inner workings of a model are often driven by a number of different theories working cooperatively. In contemporary climate modeling, for instance, elements of different theories—among them fluid dynamics, thermodynamics, electromagnetism—are put to work cooperatively. What delivers the results is not the stringent application of one theory, but the voices of different theories when put to use in chorus with each other in one model. 142
142 Frigg & Hartmann (2020).
- Hugh Everett’s thesis, Appendix II
- Suppes, P. (1961). A comparison of the meaning and uses of models in mathematics and the empirical sciences. 143
- Suppes, P. (1967). What is a scientific theory? 144
- Bunge: “Problems of Modeling” 145
- Box: “All models are wrong [, but some are useful].” 146
- Morgan, M.S. & Morrison, M. (1999). Models as Mediators. 147
- Frigg: “Surrogative Reasoning Condition” 148
- “What is the difference between a model and a theory?” - physics.stackexchange.com
- NPR: How to make sense of all the COVID-19 projections? A new model combines them.
2.7.3 Digression: Some physicists have semantic differences
- TODO: explain
- HEP theorists especially
- HEP theorists often use “theory” to mean “theoretical framework”: quantum field theory, yang-mills theory, string theory, etc.
- “Model building” in HEP means piecing together a particular theory, a “model”, using a “theory” (theoretical framework).
- The issue is purely semantic. The important point of the above discussion is that a model stands-in as a representative of a theory that can be compared with the data.
- TODO: find good example refs
- Hodges, W. (2020). Models and modelling.
- theory - nLab
2.7.4 Stylized facts
- Kaldor, N. (1961). Capital accumulation and economic growth. 149
- Abad, L.A. & Khalifa, K. (2015). What are stylized facts? 150
- Hirschman, D. (2016). Stylized facts in the social sciences. 151
- Democracies rarely go to war with each other. 152
2.8 Pseudoscience
2.8.1 The demarcation problem
- Poor quality science vs pseudoscience
- Feynman, R.P. (1974). Cargo cult science. 153
- Bunge, M. (1991). What is science? Does it matter to distinguish it from pseudoscience? A reply to my commentators. 154
- Bunge, M. (2011). Knowledge: Genuine and bogus. 155
- Pigliucci, M. & Boudry, M. (2013). Philosophy of Pseudoscience: Reconsidering the Demarcation Problem. 156
- Blancke, S. & Boudry, M. (2022). Pseudoscience as a negative outcome of scientific dialogue: A pragmatic-naturalistic approach to the demarcation problem. 157
153 Feynman (1999), p. 189.
154 Bunge (1991).
155 Bunge (2011).
156 Pigliucci & Boudry (2013).
157 Blancke & Boudry (2022).
Feynman:
Science is the belief in the ignorance of experts. When someone says “science teaches such and such”, he is using the word incorrectly. Science doesn’t teach it; experience teaches it. If they say to you science has shown such and such, you might ask, “How does science show it—how did the scientists find out—how, what, where?” Not science has shown, but this experiment, this effect, has shown. And you have as much right as anyone else, upon hearing about the experiments (but we must listen to all the evidence), to judge whether a reasonable conclusion has been arrived at. 158
158 Feynman (1999), p. 187.
2.8.2 Bullshit
- James Ladyman on Pseudoscience and Bullshit
- Smith, N. (2022). The two paper rule.
2.9 My thoughts
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
2.10 Annotated bibliography
2.10.1 Hume, D. (1748). An Enquiry Concerning Human Understanding.
- Hume (2007)
2.10.1.1 1. Of the different Species of Philosophy
2.10.1.2 2. Of the Origin of Ideas
2.10.1.3 3. Of the Association of Ideas
2.10.1.4 4. Sceptical Doubts concerning the Operations of the Understanding
2.10.1.5 5. Sceptical Solution of these Doubts
2.10.1.6 6. Of Probability
2.10.1.7 7. Of the Idea of necessary Connexion
2.10.1.8 8. Of Liberty and Necessity
2.10.1.9 9. Of the Reason of Animals
2.10.1.10 10. Of Miracles
2.10.1.11 11. Of a particular Providence and of a future State
2.10.1.12 12. Of the academical or sceptical Philosophy
2.10.1.13 My thoughts
- TODO.
2.10.2 Pigliucci, M. (2010). Nonsense on Stilts: How to Tell Science From Bunk.
- Pigliucci (2010)
2.10.2.1 My thoughts
- TODO.
2.10.3 French, S. (2007). Science: Key Concepts in Philosophy.
- S. French (2007)
2.10.3.1 1. Introduction
Do not become archivists of facts. Try to penetrate to the secret of their occurrence, persistently search for the laws which govern them.
– Ivan Pavlov
The important thing in science is not so much to obtain new facts as to discover new ways of thinking about them.
– W.L. Bragg
TODO:
- summarize
- Feynman
- Giere
- Darwin
- Einstein
2.10.3.2 2. Discovery
- Eureka moments
- Archimedes
- Kary Mullis - Nobel Prize 1993 for Polymerase Chain Reaction (PCR)
- “Eureka moments” fit well with the “romantic view” of discovery - Kant
- “In other words, discovery is ultimately irrational and unanalysable.”
- Hypothetico-deductive account of discovery
- Hypotheses arrived at via creative Eureka moments.
- (Make a number of relevant observations.)
- Verification via deductive account of observations.
- Inductive account of discovery
- (Hypotheses arrived at via creative Eureka moments.)
- Make a number of relevant observations.
- Inductively support hypotheses.
2.10.3.3 3. Heuristics
2.10.3.4 4. Justification
2.10.3.5 5. Observation
2.10.3.6 6. Experiment
2.10.3.7 7. Realism
2.10.3.8 8. Anti-realism
2.10.3.9 9. Independence
2.10.3.10 10. Gender Bias
2.10.3.11 My thoughts
- TODO.
2.10.4 More articles to do
- TODO.
2.11 Links and encyclopedia articles
2.11.1 SEP
- Abduction
- Analysis of knowledge
- Analytic/synthetic distinction
- Ancient atomism
- Aristotle’s metaphysics
- Ayer, Alfred Jules (1910-1989)
- Bacon, Francis (1561-1626)
- Bayesian epistemology
- Berkeley, George (1685-1753)
- Carnap, Rudolf (1891-1970)
- Coherentist theories of epistemic justification
- Confirmation
- Democritus (460-370 BCE)
- Descartes, René (1596-1650)
- Descartes’ epistemology
- Descartes’ method
- Einstein’s Philosophy of Science
- Epistemological problems of perception
- Epistemological problems of testimony
- Epistemology
- Formal epistemology
- Foundationalist theories of epistemic justification
- Galileo Galilei (1564-1642)
- Gassendi, Pierre (1592-1655)
- Grosseteste, Robert (ca. 1168-1253)
- Historicist theories of scientific sationality
- Hobbes, Thomas (1588-1679)
- Hobbes’ philosophy of science
- Hume, David (1711-1776)
- Ibn Sina (980-1037)
- Identity of Indiscernibles
- Induction, The problem of
- Internalist vs. externalist conceptions of epistemic justification
- Kant, Immanuel (1724-1804)
- Kant’s account of reason
- Kant’s critique of metaphysics
- Kant’s transcendental arguments
- Laws of nature
- Leibniz, Gottfried Wilhelm (1646-1716)
- Leibniz’s influence on Kant
- Leibniz’s philosophy of physics
- Leibniz’s modal metaphysics
- Locke, John (1632-1704)
- Locke’s philosophy of science
- Mach, Ernst (1838-1916)
- Measurement in science
- Mechanisms in science
- Miracles
- Naturalized epistemology
- Newton, Isaac (1642-1727)
- Newton’s philosophy
- Newton’s Philosophiae Naturalis Principia Mathematica
- Ockham, William of (1287-1347)
- Parmenides
- Popper, Karl (1902-1994)
- Presocratic philosophy
- Principle of sufficient reason
- Pythagoras (570-495 BCE)
- Pythagoreanism
- Rationalism vs. empiricism
- Reid, Thomas (1710-1796)
- Reproducibility of scientific results
- Science and pseudo-science
- Scientific explanation
- Scientific method
- Skepticism
- Socrates (469-399 BCE)
- Spinoza, Baruch (1632-1677)
- Statistics, Philosophy of
- Thought experiments
2.11.2 IEP
- A priori and a posteriori
- Berkeley, George (1685-1753)
- Carnap, Rudolf (1891-1970)
- Contemporary Metaphilosophy
- Democritus (460-370 BCE)
- Epistemology
- Epistemology of testimony
- Explanation
- Gettier problems
- Hempel, Carl Gustav (1905-1997)
- Hume, David (1711-1776)
- Ibn Sina (980-1037)
- Induction, Problem of
- Internalism and externalism in epistemology
- Locke, John (1632-1704)
- Naturalism
- Naturalistic epistemology
- Parmenides
- Peirce, Charles Sanders (1839-1914): Logic
- Plato (428/7 or 424/3 - 348/7 BCE)
- Plato’s Academy (387 BCE - 529 CE)
- Popper, Karl (1902-1994): Philosophy of Science
- Problem of the Criterion
- Pythagoras (570-495 BCE)
- Reductionism
- Safety condition for knowledge
- Simplicity in the philosophy of science
- Skepticism, Ancient Greek
- Skepticism, Contemporary
- Socrates (469-399 BCE)
- Spinoza, Baruch (1632-1677): Metaphysics
- Thales of Miletus (c. 624/623-548/545 BCE)
- William of Ockham (1280-1349)
2.11.3 Wikipedia
- Abductive reasoning
- Academy of Gondishapur
- Alhazen AKA Ibn al-Haytham (965-1040)
- Ampère, André-Marie (1775-1836)
- Analytic/synthetic distinction
- Ancient higher-learning institutions
- A priori and a posteriori
- Archimedes (c. 287-212 BCE)
- Aristarchus of Samos (310-230 BCE)
- Aristotle (384-322 BCE)
- Aumann’s agreement theorem
- Babbage, Charles (1791-1871)
- Bacon, Francis (1561-1626)
- Baconian method
- Bacon, Roger (1214-1292)
- Berkeley, George (1685-1753)
- Bohr, Niels (1885-1962)
- Boltzmann, Ludwig (1844-1906)
- Bootstrapping
- Born, Max (1882-1970)
- Boyle, Robert (1627-1691)
- Carnap, Rudolf (1891-1970)
- Carnot, Nicolas Léonard Sadi (1796-1832)
- Cartesian doubt
- Cauchy, Augustin-Louis (1789-1857)
- Copernicus, Nicolaus (1473-1543)
- Copernican Revolution
- Cramér-Rao bound
- Critical thinking
- Curie, Marie (1867-1934)
- Dalton, John (1766-1844)
- Darwin, Charles (1809-1882)
- da Vinci, Leonardo (1452-1519)
- de Broglie, Louis (1892-1987)
- Deductive-nomological model
- Democritus (460-370 BCE)
- Descartes, René (1596-1650)
- Dewey, John (1859-1952)
- Dirac, Paul (1902-1984)
- Einstein, Albert (1879-1955)
- Empiricism
- Epicurus (341-270 BCE)
- Epistemology
- Eratosthenes (276-195/194 BCE)
- Euclid (fl. 300 BCE)
- Euler, Leonhard (1707-1783)
- Evolution
- Evolution, Introduction to
- Evolution, Outline of
- Explanation
- Faraday, Michael (1791-1867)
- Fisher, Ronald (1890-1962)
- Franklin, Benjamin (1706-1790)
- Fraunhofer, Joseph von (1787-1826)
- Galileo Galilei (1564-1642)
- Gassendi, Pierre (1592-1655)
- Gauss, Carl Friedrich (1777-1855)
- Gettier problem
- Grosseteste, Robert (ca. 1168-1253)
- Halley, Edmond (1656-1742)
- Hamilton, William Rowan (1805-1865)
- Heisenberg, Werner (1901-1976)
- Herschel, John (1792-1871)
- Hilbert, David (1862-1943)
- History of science
- History of the scientific method
- Hobbes, Thomas (1588-1679)
- House of Wisdom
- Human evolution
- Human migrations, Early
- Hume, David (1711-1776)
- Hume’s fork
- Huxley, Thomas Henry (1825-1895)
- Hypothetico-deductive model
- Ibn al-Haytham (965-1040) AKA “Alhazen”
- Ibn Sina (980-1037)
- Induction, The problem of
- Inductivism
- Interval estimation
- Ionian Enlightenment
- Islamic Golden Age
- Jacobi, Carl Gustav Jacob (1804-1851)
- Jordan, Pascual (1902-1980)
- Justification, Theory of
- Kelvin, William Thomson (1824-1907)
- Knowledge
- Ladd-Franklin, Christine (1847-1930)
- Lagrange, Joseph-Louis (1736-1813)
- Laplace, Pierre-Simon (1749-1827)
- Leibniz, Gottfried Wilhelm (1646-1716)
- Leibniz-Newton calculus controversy
- Likelihood principle
- Locke, John (1632-1704)
- Lucretius (99-55 BCE)
- Mach, Ernst (1838-1916)
- Maxwell, James Clerk (1831-1879)
- Mendel, Gregor (1822-1884)
- Mill, John Stuart (1806-1873)
- Mill’s Methods
- Models of scientific inquiry
- Mozi (470-391 BCE)
- Natural philosophy
- Naturalized epistemology
- Neptune, Discovery of
- Neyman, Jerzy (1894-1981)
- Neyman-Pearson lemma
- Newton, Isaac (1642-1727)
- Neurath, Otto (1882-1945)
- Neurath’s boat
- Ockham, William of (1287-1347)
- Outline of science
- Outline of scientific method
- Parmenides
- Pauli, Wolfgang (1900-1958)
- Pearson, Egon (1895-1980)
- Pearson, Karl (1857-1936)
- Peirce, Charles Sanders (1839-1914)
- Philosophiæ Naturalis Principia Mathematica (1687)
- Phlogiston theory
- Planck, Max (1858-1947)
- Plato (428/7 or 424/3 - 348/7 BCE)
- Platonic Academy (387 BCE - 529 CE)
- Plato’s analogy of the divided line
- Plato’s problem from Noam Chomsky
- Poincaré, Henri (1854-1912)
- Popper, Karl (1902-1994)
- Principle of sufficient reason
- Pseudoscience
- Pseudoscience, List of topics characterized as
- Pythagoras (570-495 BCE)
- Pythagoreanism
- Razor (philosophy)
- Reid, Thomas (1710-1796)
- Renaissance
- Russell, Bertrand (1872-1970)
- Scholasticism
- Schrödinger, Edwin (1887-1961)
- Science
- Science, Philosophy of
- Scientific skepticism
- Scientific method
- Scientism
- Skepticism, Philosophical
- Socrates (469-399 BCE)
- Somerville, Mary (1780-1729)
- Spinoza, Baruch (1632-1677)
- Statistical classification
- Statistical hypothesis testing
- Statistical inference
- Statistical sensitivity and specificity
- Statistical significance
- Statistics
- Statistics, Founders of
- Statistics, History of
- Statistics, Outline of
- Statistics, Philosophy of
- Superseded scientific theories
- Systematic error
- Thales of Miletus (c. 624/623-548/545 BCE)
- Timeline of the history of the scientific method
- Timeline of scientific thought
- Tukey, John (1915-2000)
- Type-I and type-II errors
- Uniformitarianism
- Unsolved problems in statistics, List of
- Volta, Alessandro (1745-1827)
- von Neumann, John (1903-1957)
- Whewell, William (1794-1866)
- Wolff, Christian (1679-1754)
- Xenophanes (c. 570-478 BCE)
- Xenophon (c. 431-354 BCE)
2.11.4 Others
- Accommodationism - RationalWiki.org, coined by Austin Dacey
- Holmesian fallacy
- Hume’s fork - mathmonism.com
- Inference to the Best Explanation - informationphilosopher.com
- Is Hume’s fork self-refuting? - Philosophy StackExchange
- Scientism - RationalWiki.org
- Newton’s Flaming Laser Sword - Mike Alder, Philosophy Now
- Aldrich, John. (?). Earliest uses of symbols of calculus.
- Suber, P. (2003). Guide to Philosophy on the Internet.
- Starbird, M. (2016). Who invented calculus?
- DeMichele, T. (2017). A priori-a posteriori, analytic-synthetic, and necessary-contingent distinctions.
- Alsabeh, F. (2018). Kant, demystified.
- Stearns, P. (2020). Epistemology: A priori vs. a posteriori, analytic vs. synthetic, necessary vs. contingent.