Philosophy of mathematics

These next several outlines deal with philosophy of certain specialized topics, starting with this one on the philosophy of mathematics. Here we dig into issues of what is abstraction.

First we survey the following branches of mathematics: algebra, analysis, numbers theory, logic, model theory, and category theory. Then we discuss unification programs across branches, followed by sections on positions in philosophy of mathematics, in particular dealing with the realism/antirealism or platonism/nominalism debate.

Contents

1. Algebra
   1. Introduction
   2. History
   3. Linear algebra
   4. Finite groups
   5. Lie groups
   6. Abstract algebra
   7. More
2. Analysis
   1. Introduction
   2. History
   3. Development of calculus
   4. Differential geometry
3. Number theory
   1. Introduction
   2. Set theory
   3. Transfinite numbers
4. Logic
   1. Introduction
   2. History
   3. Propositional logic
   4. First-order logic
   5. Second-order logic
   6. Modal logic
   7. Alternative logics
   8. Proof theory
5. Model theory
   1. Introduction
   2. History
   3. Incompleteness
   4. Complexity theory
6. Category theory
   1. Introduction
   2. History
   3. Homotopy type theory
   4. Cobordism hypothesis
   5. Topos theory
   6. Applications
7. Unification programs
   1. Introduction
   2. Erlangen program
   3. Langlands program
   4. Univalent foundations
8. Platonism
   1. Introduction
   2. Pythagoreanism
   3. Plato
   4. Contemporary platonism
   5. Visual proofs
9. Nominalism
   1. Introduction
   2. History
   3. Science Without Numbers
10. Logicism
    1. Introduction
    2. Principia Mathematica
    3. ZFC
    4. Neologicism
11. Formalism
    1. Introduction
    2. Hilbert’s program
12. Intuitionism
    1. Introduction
    2. Linear logic
    3. Criticism
13. Fictionalism
14. Structuralism
15. Naturalism
    1. Unreasonable effectiveness
    2. Quine-Putnam indispensability thesis
    3. Mathematical naturalism
16. My thoughts
17. Annotated bibliography
    1. Wigner, E.P. (1960). The Unreasonable Effectiveness of Mathematics in the Natural Sciences.
    2. Field, H. (1980). Science Without Numbers.
    3. Snapper, E. (1979). The Three Crises in Mathematics: Logicism, Intuitionism, Formalism.
    4. More articles to do
18. Links and encyclopedia articles
    1. SEP
    2. IEP
    3. Wikipedia
    4. Others
    5. Videos
19. References

Algebra

Introduction

TODO

Prove all things; hold fast that which is good.

– 1 Thessalonians, 5:21–28, KJV

History

• roots from Babylonians
• Al-Karaji (c. 953-1029)
• Gerolamo Cardano (1501-1576)
• Carl Friedrich Gauss (1777-1855)
  • published a proof of the fundamental theorem of algebra (1797)
  • The theorem states that the field of complex numbers is algebraically closed.
• Évariste Galois (1811-1832)
• Arthur Cayley (1821-1895)
• Leopold Kronecker (1823-1891)
• arithmetic vs abstract algebra

Linear algebra

• Linear equations and transformation
• Vector spaces and dual spaces
  • For an infinite dimensional vector space, V, while elements of V must have “finite support” (only finitely many nonzero coordinates in any basis representation), elements of V* can have “infinite support.”
• Axler, S. (2024). Linear Algebra Done Right.
• Spectral theorem: \(A\) is normal, \(A A^\dagger = A^\dagger A \iff A = U D U^\dagger\) is an eigendecomposition of \(A\), where the column vectors of \(U\) are the eigenvectors of \(A\) with corresponding eigenvalues on the diagonal of \(D\).
• Principal Component Analysis (PCA)
• Rayleigh quotient

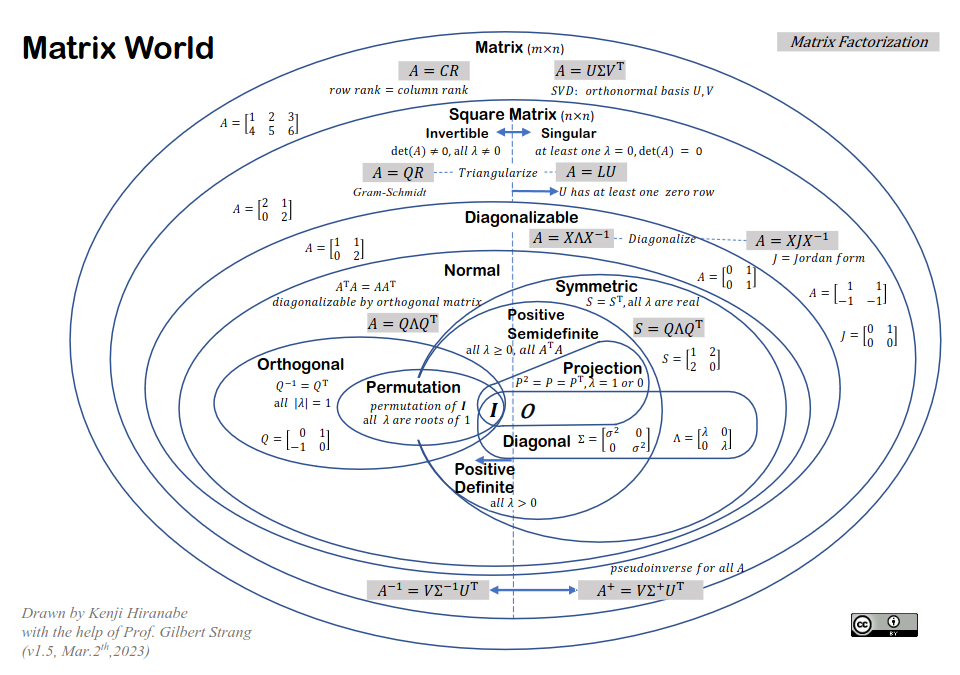
See also:

• Estimation of covariance matrices
• Convex optimization

Finite groups

• Group
• Sporadic group
• Classification of finite simple groups
• Elwes, R. (2006). An enormous theorem: The classification of finite simple groups.
• There are 26 sporadic simple groups (27 if you count the Tits group).
• YouTube 3Blue1Brown: Group theory and why I love
  808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000.
• Monstrous moonshine
• Richard Borcherds (b. 1959)
• Carter, N. (2009). Visual Group Theory.¹

Lie groups

• Lie group
  • Sophus Lie (1842-1899)
  • Élie Cartan (1869-1951)
  • Schwichtenberg, J. (2016). Classification of simple Lie groups.
  • Hall, B.C. (2000). An Elementary Introduction to Groups and Representations.²
  • Zee, A. (2016). Group Theory in a Nutshell for Physicists.³
• Dynkin diagrams
  • ADE classification
  • Siegel, K. (2014). The ubiquity of ADE classifications in nature.

Abstract algebra

• A field is a commutative division ring.
• Vector space
• Modules are to rings as vector spaces are to fields.

More

• Jordan algebras
  • McCrimmon, K. (2000). A Taste of Jordan Algebras.⁴
• Algebraic number theory
• Representation theory
• Langlands program
• Universal algebra
• Hurwitz’s theorem
  • The real numbers, the complex numbers, the quaternions, and the octonions exhaust all the possible normed division algebras.
  • Baez, J.C. (2002). The octonions.⁵
  • Westbury, B.W. (2010). Hurwitz’ theorem on composition algebras.⁶

See also:

• Foundations of QM
• Supersymmetry in the Outline of physics

Analysis

Introduction

TODO

History

• René Descartes (1596-1650)
  • Geometry and coordinates, modern notation, geometric problems forumalted with algebra
  • La Géométrie (1637)
• Isaac Newton (1642-1726/7)
• Gottfried Wilhelm Leibniz (1646-1716)
• Jacob Bernoulli (1655-1705)
• Leonhard Euler (1707-1783)
  • Mechanica (1736)
• Pierre-Simon Laplace (1749-1827)
• Carl Friedrich Gauss (1777-1855)
• Augustin-Louis Cauchy (1789-1857)
• Karl Weierstrass (1815-1897)
• George Stokes (1819-1903)
• Differential forms
• Geometry and the Erlangen program

Development of calculus

• James Gregory (1638-1675)
• Isaac Barrow (1630-1677)
  • Fundamental theorem of calculus in Proposition 11, Lecture 10, of his Lectiones Geometricae, published in 1670.
• Isaac Newton (1642-1727)
  • Newton claimed to have the ideas of calculus in the mid 1660s.
  • In 1669, Newton wrote an article on infinite series with ideas leading to calculus: “De analysi per aequationes numero terminorum infinitas,” which wasn’t published until 1711, 42 years later.
  • Philosophiæ Naturalis Principia Mathematica (1687)
• Gottfried Wilhelm Leibniz (1646-1716)
  • Leibniz first used \(dx\) in publication in
    Leibniz, G.W. (1684). Nova methodus pro maximis et minimis. Acta Eruditorum.
  • Leibniz first used his intergral sign, \(\int\), in publication in
    Leibniz, G.W. (1686). De geometria recondita et analysi indivisibilium atque infinitorum. Acta Eruditorum.
  • Wolfram, S. (2013). Dropping in on Gottfried Leibniz.
• Aldrich, John. (?). Earliest uses of symbols of calculus.
• Leibniz-Newton calculus controversy
  • In 1849, C. I. Gerhardt, while going through Leibniz’s manuscripts, found extracts from Newton’s “De analysi per aequationes numero terminorum infinitas.”
  • Starbird, M. (2016). Who invented calculus?

Matrix calculus

• Matrix calculus
• Dwyer, P.S. (1967). Some applications of matrix derivatives in multivariate analysis.⁷

Differential geometry

• History
  • Leonhard Euler (1707-1783)
  • William Rowan Hamilton (1805-1865)
  • George Stokes (1819-1903)
  • Josiah Willard Gibbs (1839-1903)
  • Élie Cartan (1869-1951)
  • W.V.D. Hodge (1903-1975)
• Vector calculus
  • Stokes’ theorem
  • Tong, D. (2022). Lectures on Vector Calculus.
• Differential forms
  • Manifold, tangent and cotangent spaces, vector bundle, fiber bundle
  • Burke, W.L. (1985). Applied Differential Geometry.⁸
  • Frankel, T. (1997). The Geometry of Physics: An Introduction.⁹
  • Review by Frè¹⁰
  • Varadarajan, V. S. (2003). Vector bundles and connections in physics and mathematics: some historical remarks.¹¹
  • Tao, T. (2007). Differential forms and integration.¹²
  • Sussman, G.J. & Wisdom, J. (2013). Functional Differential Geometry.¹³
  • Tu, L.W. (2017). Differential Geometry: Connections, Curvature, and Characteristic Classes.¹⁴
  • Bronstein, M.M. et al. (2021). Geometric deep learning: Grids, groups, graphs, geodesics, and gauges.¹⁵
• De Rham cohomology
• Chern-Simons theory
• Non-commutative
  • Connes, A. (1985). Non-commutative differential geometry.¹⁶

\[ a \times b = \star(a \wedge b) \]

See also:

• Fiber bundles

Number theory

Introduction

• Peano axioms
• Robinson arithmetic
• Newstead, C. (2022). An Infinite Descent into Pure Mathematics.

Set theory

• Membership: Axiom of extensionality
• von Neumann’s set theoretical definition of numbers

Naive Set Theory

• Axiom of unrestricted comprehension
  • There exists the set \(\{ x : \phi(x) \}\), the set whose members are those that satisfy \(\phi\).
• Russell’s paradox
  • Let \(y = \{ x : x \notin x \}\) then \(y \in y \Leftrightarrow y \notin y\)
• Curry’s paradox

Zermelo-Fraenkel set theory

• Zermelo-Fraenkel set theory
• Axiom schema of specification AKA Axiom of restricted comprehension
  • Define a set by defining a subset of a known set \(A\), \(\{ x \in A : \phi(x) \}\), instead of the more general \(\{ x : \phi(x) \}\)
  • Given any set A, there exists a subset of \(A\), whose memebers are those that satisfy \(\phi\) (and are also members of \(A\)).
• Zermelo-Fraenkel set theory + Axiom of choice = ZFC

Other approaches

• Von Neumann-Bernays-Gödel set theory
• Quine’s New Foundations

Transfinite numbers

• Ordinal (index) vs cardinal (size) numbers
• Cantor-Bernstein-Schröeder theorem
• Transfinite numbers:
  • \(\omega\): the smallest transfinite ordinal number; the order type of the natural numbers.
  • \(\aleph_0\): the first transfinite cardinal number; the cardinality of the natural numbers, \(\aleph_0 \equiv |\mathbb{N}|\)
  • There is a one-to-one correspondence between ordinal and cardinal numbers.¹⁷ \(\omega = \aleph_0\)
    
  • The \(\aleph_n\) hierarchy of cardinals is defined by transfinite recursion:
    • \(\aleph_0\) is the smallest infinite cardinal.
    • \(\aleph_{n+1}\) is the successor cardinal to \(\aleph_{n}\)
    • \(\aleph_{\lambda} = \mathrm{sup}_{n<\lambda} \aleph_n\) for limit ordinals \(\lambda\)
  • \(\aleph_0\) is the smallest infinite cardinal; it is countable.
  • \(\aleph_1\) is the first uncountable cardinal.
  • \(\aleph_2\) is the second uncountable cardinal.
• Transfinite numbers were anticipated by Robert Grosseteste (ca. 1168-1253).
• Developed by Georg Cantor (1845-1918) in 1895
  • Cantor’s first set theory article
  • Proved that the real numbers are uncountably infinite.
  • The cardinalities of \(\mathbb{R}\) and \(\mathbb{R}^n\) are both \(C\).
• Cantor’s theorem
  • Let \(|A| \equiv \mathrm{card}(A)\) denote the cardinality (i.e size) of a set, \(A\).
  • A power set, \(P(A)\), of a set, \(A\), is the set of all subsets of \(A\).
  • The cardinality of a power set is \(|P(A)| = 2^{|A|}\)
  • The cardinality of a power set is strictly larger than the set: \(|A| < |P(A)|\)
• Cardinality of the continuum
  • The cardinality of the reals: \(C \equiv |\mathbb{R}|\)
  • Examples of sets with cardinality = \(C\)
    • real numbers, \(\mathbb{R}\)
    • closed or open intervals on \(\mathbb{R}\)
    • Euclidean space, \(\mathbb{R}^n\)
    • complex numbers, \(\mathbb{C}\)
    • set of all continuous functions from \(\mathbb{R}\) to \(\mathbb{R}\)
    • power set of of natural numbers, \(P(\mathbb{N})\)
  • The cardinality of the reals is the power set of the natural numbers: \(C \equiv |\mathbb{R}| = |P(\mathbb{N})| = 2^{|\mathbb{N}|} = 2^{\aleph_0} > \aleph_0\)
• Continuum Hypothesis (CH)
  • CH: There is no set \(S\) such that \(\aleph_0 < |S| < 2^{\aleph_0}\)
  • \(C = 2^{\aleph_0}\), and under CH, \(C = 2^{\aleph_0} = \aleph_1\).
  • Relationship with the axiom of choice
  • Paul Cohen showed the CH is undecidable in ZFC (1963).
• Generalized Continuum Hypothesis (GCH)
  • \(\aleph_{n+1} = 2^{\aleph_n}\)

Hilbert:

There is, however, a completely satisfactory way of avoiding the paradoxes without betraying our science. The desires and attitudes which help us find this way and show us what direction to take are these:

1. Wherever there is any hope of salvage, we will carefully investigate fruitful definitions and deductive methods. We will nurse them, strengthen them, and make them useful. No one shall drive us out of the paradise which Cantor has created for us.
2. We must establish throughout mathematics the same certitude for our deductions as exists in ordinary elementary number theory, which no one doubts and where contradictions and paradoxes arise only through our own carelessness.¹⁸

Logic

Introduction

Pedagogy:

• Hunter, G. (1971). Metalogic: An Introduction to the Metatheory of Standard First-Order Logic.¹⁹
• Monk, J.D. (1976). Mathematical Logic.²⁰
• Sullivan, B.W. (2013). Everything You Always Wanted To Know About Mathematics.²¹
• Smith, P. (2020). An Introduction to Formal Logic.²²
• Smith, P. (2022). Beginning Mathematical Logic A Study Guide.²³

More:

• Carnap, R. (1958). Introduction to Symbolic Logic and its Applications.²⁴
• Teller, P. (1989). A Modern Formal Logic Primer.²⁵
• Bonevac, D. (2003). Deduction: Introductory to Symbolic Logic.²⁶
• MacFarlane, J. (2021). Philosophical Logic: A Contemporary Introduction.²⁷
• The Open Logic Text²⁸
• logicinaction.org
• logicmatters.net

History

• Aristotle (384-322 BCE)
  • founded logic
  • Square of opposition
  • Modus ponens, modus tollens, Affirming the consequent, Proof by contrapositive
• Euclid (fl. 300 BCE)
  • logico-deductive method founded by Euclid’s Elements
• Chrysippus (c. 279-206 BCE)
• Vasubandhu (fl. 4th to 5th century CE)
• Dignāga (c. 480-540 CE)
• Charles Sanders Peirce (1839-1914)
• Gottlob Frege (1848-1925)
  • Begriffsschrift (1879)
• Alfred North Whitehead (1861-1947) and Bertrand Russell (1872-1970) published Principia Mathematica in 1910
  • Russell’s paradox
  • PM avoids Russell’s paradox by introduction of the “ramified theory of types.”
  • Later lead to Church’s (1976) formulation of the logic of PM with \(r\)-types.
• Henry M. Sheffer (1882-1964)
  • Sheffer, H.M. (1913). A set of five independent postulates for Boolean algebras, with application to logical constants.²⁹
  • Propositional logic can be formulated using a single connective: either logical NAND or its dual, logical NOR.
• Emil Post (1897-1954)
• Alfred Tarski (1901-1983)
• Kurt Gödel (1906-1978)
  • Gödel’s completeness theorem (1929)
  • Gödel’s incompleteness theorems (1931)
• Gerhard Gentzen (1909-1945)
• Leon Henkin (1921-2006)

Propositional logic

• Propositional logic
  • AKA propositional calculus and zeroth-order logic
• Validity and soundness:
  • An argument is valid iff for any assignment of the truth values in the argument where all of the premises are true, the conclusion is always true.
  • An argument is sound iff it is valid and all of its premises are true.
• Sequent calculus

Syntactic consequence:

\[ A \vdash B \]

means that \(B\) is logically derivable/provable from \(A\); \(B\) is a theorem of the premises, \(A\).

Semantic consequence:

\[ A \models B \]

means that in all possible valuations in which \(A\) is true, \(B\) is also true. One says that \(A\) “entails” \(B\), or \(A\) “models” \(B\).

Note that \(\vdash\), \(\models\), and \(\equiv\) are all metalogical symbols, not part of the rules of logic; they are shorthands.

\(\vdash\) means “from which, it is derivable that.”
\(\models\) means “entails that, i.e. in every case this is true, that is true (regardless of provability).”
\(\equiv\) means “is identical to.”

Lecture notes on soundness and completeness:

• Cornell
• Waterloo

A formal system is sound if everything that is provable is in fact true, i.e. if \(A_1, A_2, \ldots A_n \vdash B\), then \(A_1, A_2, \ldots A_n \models B\).

A formal system is complete if everything that is true has a proof, i.e. if \(A_1, A_2, \ldots A_n \models B\), then \(A_1, A_2, \ldots A_n \vdash B\).

Propositional logic was proven to be sound (\(\vdash\) implies \(\models\)) and complete (\(\models\) implies \(\vdash\)) by Emil Post in 1921.³⁰

• Emil Post and his anticipation of Gödel and Turing³¹

Material implication:

\[ P \rightarrow Q \equiv \lnot P \lor Q \]

• Paradoxes of material implication
• Vacuous truth
• von Fintel, K. (2011). Conditionals.³²

Modus ponens:

\[ P \rightarrow Q, P \vdash Q \]

Modus tollens:

\[ P \rightarrow Q, \lnot Q \vdash \lnot P \]

Peirce’s law:

\[ ((P \rightarrow Q) \rightarrow P) \rightarrow P \]

• TODO: More basic examples in propositional logic
• TODO: Use-mention distinction: P vs ‘P’ vs Quine quotes
• Cut-elimination theorem
• Gerhard Gentzen (1909-1945)

First-order logic

• First-order logic
  • AKA predicate logic
  • Domain of discourse: \(\{x\}\)
  • Adds (non-logical) predicates, \(Fx\), and quantification over elements, \(\exists x\ Fx\).
• C.S Peirce was first to distinguish between propositional logic, first-order logic, and second-order logic in 1885.³³
• Consistency, completeness, expressivity
• Gödel’s completeness theorem
  • Establishes a correspondence between semantic truth and syntactic provability in first-order logic.
  • Gödel, K. (1929). Über die Vollständigkeit des Logikkalküls.³⁴
    • His doctoral dissertation, University Of Vienna.
    • The first proof of the completeness theorem.
  • Henkin, L. (1996). The discovery of my completeness proofs.³⁵
  • Awodey, S. & Forssell, H. (2013). First-order logical duality.³⁶
  • Lindström’s theorem
• Presburger arithmetic
  • First-order theory of the natural numbers with addition, but without multiplication.
  • Presburger arithmetic is consistent, complete, and decidable.

Limitations

• Löwenheim-Skolem theorem
  • The Löwenheim-Skolem theorem implies that infinite structures cannot be categorically axiomatized in first-order logic.
  • No first-order theory has the strength to uniquely describe a structure with an infinite domain, such as the natural numbers or the real line.
• In second-order logic, it is possible to define the addition and multiplication operations from the successor operation, but this cannot be done in the more restrictive setting of first-order logic.
  • TODO: show this.
  • Bès, A. (2002). A survey of arithmetical definability.³⁷
  • Bès, A. & Choffrut, C. (2022). Decidability of definability issues in the theory of real addition.³⁸
• Tennenbaum’s theorem
• Quantifiers other than \(\forall\) and \(\exists\) are only definable within second-order logic or higher-order logics.

See also:

• Number theory

Second-order logic

• Second-order logic
• Second-order and higher-order logic, SEP
• Includes relation variables in addition to object variables and allows quantification over both.
  • Extends first-order logic to allow predicates having predicates or functions as arguments, or in which one or both of predicate quantifiers or function quantifiers are permitted.
  • \(\exists P\ P(x)\)
• Addition and multiplication are definabile in second-order logic.
  • Peano arithmetic, PA
  • Second-order arithmetic, \(\mathrm{Z}_{2}\)
• The power set can be written in terms of second-order logic.
  • This second-order expressibility of the power-set operation permits the simulation of higher-order logic within second order.³⁹
• \(\mathbb{N} \models \mathrm{PA}\)
  • The natural numbers model PA, but not uniquely in FOL.
  • In SOL, PA is categorical, meaning it has only one model up to isomorphism.
• Henkin semantics
  • SOL with Henkin semantics is complete.⁴⁰
• Higher-order logics, type theory
  • Russell’s theory of types⁴¹
  • Alonzo Church’s lambda calculus⁴²
  • All higher-order logics have the same expressive power as second-order logic.
  • Modern type theory and its relationship with category theory

Incompleteness of second-order logic

• Second-order logic opens the door to Gödel’s incompleteness theorems.
• According to Gödel’s incompleteness theorems, the theory of PA (if consistent) is incomplete.
• Kleene, S.C. (1943). Recursive predicates and quantifiers.⁴³
  • The incompleteness of second-order logic is deeply related to recursion.
• Rossberg, M. (2004). First-order logic, second-order logic, and completeness.⁴⁴

See also:

• Model theory
• Incompleteness

Discussion

• Michael Dummett
• S.C. Kleene
  • Kleene, S.C. (1952). Introduction to Metamathematics.⁴⁵
    • First formulation of the sequent calculus in the modern style
• Setwart Shapiro
  • Foundations without Foundationalism: A Case for Second-Order Logic (1991)⁴⁶
• Gillian Russell
  • Russell, G. (2015). The justification of the basic laws of logic.⁴⁷
• Eliezer Yudkowsky
  • Second-Order Logic: The Controversy
  • “Second-order logic is sound, in the sense that anything syntactically provable from a set of premises, is true in any model obeying those premises. But second-order logic isn’t complete; there are semantic consequences you can’t derive. If you take second-order logic at face value, there’s no effectively computable way of deriving all the consequences of what you say you ‘believe’… which is a major reason some mathematicians are suspicious of second-order logic. What does it mean to believe something whose consequences you can’t derive?”
• George Boolos
  • Boolos, G. (1984). To be is to be the value of a variable (or to be some values of some variables).⁴⁸
  • Plural quantification
• Ethan Jerzak
  • Jerzak, E. (2009). Second-order logic, or: How I learned to stop worrying and love the incompleteness theorems.⁴⁹
• Otávio Bueno
  • Bueno, O. (2010). A defense of second-order logic.⁵⁰
• Ted Sider
  • Sider, T. (2022). Crash course on higher-order logic.⁵¹

Modal logic

• C.I. Lewis (1883-1964)
  • Founded modern modal logic.
  • Criticism of material implication. Introduced strict implication.⁵²
  • Strict implication is not truth-functional. It requires asking about the truth-values that propositions take in worlds other than the actual world.
• Rudolf Carnap (1891-1970)
  • Carnap, R. (1947). Meaning and Necessity.⁵³
• Saul Kripke (1940-2022)
  • Kripke, S.A. (1959). A completeness theorem in modal logic.⁵⁴
  • Revives Leibniz’s idea that necessity is truth in all possible worlds.
• David Lewis (1941-2001)
  • On the Plurality of Worlds (1986)⁵⁵

\(\Box\) means “necessarily.” \(\Diamond\) means “possibly.”

If necessarily \(P\), then necessarily necessarily \(P\):

\[ \Box P \rightarrow \Box \Box P \]

De Morgan duality:

\[ \Diamond P = \lnot \Box \lnot P \]

\[ \Box P = \lnot \Diamond \lnot P \]

More:

• Security logic
• De dicto and de_re

Alternative logics

• Liar paradox
  • Carroll, L. (1895). What the tortoise said to Achilles.⁵⁶
• Intuitionistic Logic
  • Law of excluded middle (LEM), Tertium non datur:
    \(\vdash A \lor \lnot A\)
  • Law of double negation (LDN):
    \(\lnot \lnot A \leftrightarrow A\)
  • Intuitionistic logic rejects LEM and LDN.
  • Constructive mathematics
• Paraconsistent logic
  • Principle of explosion
  • Ex contradictione quodlibet (ECQ): from a contradiction anything follows.
    \(A, \lnot A \models B\)
  • Law of No Contradiction (LNC).
    \(\models \lnot ( A \land \lnot A )\)
  • Paraconsistent logics reject ECQ, and may or may not invalidate LNC.
  • Dialetheism rejects LNC.
  • Priest, G. (1998). What is so bad about contradictions?⁵⁷
  • Martínez-Ordaz, M. del R. (2021). The ignorance behind inconsistency toleration.⁵⁸

Criticism:

• Quine, W.V.O. (1986). Philosophy of Logic.⁵⁹

See also:

• Intuitionism

Proof theory

• Curry-Howard correspondence
• Proof-theoretic semantics
• Realizability
• Viteri, S. & DeDeo, S. (2022). Epistemic phase transitions in mathematical proofs.⁶⁰

See also:

• Category theory
• Complexity theory
• Hilbert’s program
• Logicism
• Formalism

Model theory

Introduction

• Wikipedia: Model theory
• Hodges:⁶¹
  • model theory = universal algebra + logic
  • model theory = algebraic geometry - fields
• SEP: Model theory
  • Model theory is the study of the interpretation of any language, formal or natural, by means of set-theoretic structures, with Alfred Tarski’s truth definition as a paradigm.

Hunter:

Model theory is the theory of interpretations of formal languages (a model of a formula of a language is an interpretation of the language for which the formula comes out true).⁶²

Weiss & D’Mello:

Model Theory is the part of mathematics which shows how to apply logic to the study of structures in pure mathematics.⁶³

Pedagogy:

• Weiss, W. & D’Mello, C. (2015). Fundamentals of Model Theory.⁶⁴
• Button, T. & Walsh, S. (2018). Philosophy and Model Theory.⁶⁵

More:

• Model theory - nLab
• Formal epistemology
• Makowsky, J.A. (1995). The impact of model theory on theoretical computer science.⁶⁶

See also:

• Formal epistemology

History

• William Rowan Hamilton (1805-1865)
• Alfred North Whitehead (1861-1947)
  • Whitehead, A.N. (1898). A Treatise on Universal Algebra.
• Löwenheim-Skolem theorem (1915, 1920)
• Rudolf Carnap (1891-1970)
• Alfred Tarski (1901-1983)
• Kurt Gödel (1906-1978)
• Leon Henkin (1921-2006)
• Jaakko Hintikka (1929-2015)
• Wilfrid Hodges (b. 1941)
  • Hodges, W. (1985). Truth in a structure.⁶⁷

Incompleteness

• Kurt Gödel (1906-1978)
  • Carnap inspired Gödel to study logic.⁶⁸
• Gödel, K. (1931). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I.⁶⁹
• Gödel, K. (1951). Some basic theorems on the foundations of mathematics and their implications.⁷⁰
• Gödel presented his incompleteness theorems at the Second Conference on the Epistemology of the Exact Sciences in Königsberg September 5-7, 1930.
  • von Neumann recognized the importance first.
  • Carnap had warning of Gödel’s results the month before.⁷¹
• Goldstein⁷²

Fom the SEP:

The first incompleteness theorem states that in any consistent formal system \(F\) within which a certain amount of arithmetic can be carried out, there are statements of the language of \(F\) which can neither be proved nor disproved in \(F\). According to the second incompleteness theorem, such a formal system cannot prove that the system itself is consistent (assuming it is indeed consistent).⁷³

Related:

• Tarski’s undefinability theorem on the formal undefinability of truth
  • Tarski, A. (1936). The concept of truth in formalized languages.⁷⁴
  • Tarski, A. (1969). Truth and proof⁷⁵
• Church’s proof that Hilbert’s Entscheidungsproblem is unsolvable
  • Church, A. (1936). A note on the Entscheidungsproblem.⁷⁶
• Turing’s theorem that there is no algorithm to solve the halting problem
  • Turing, A.M. (1937). On computable numbers, with an application to the Entscheidungsproblem.⁷⁷
• Rice’s theorem that all non-trivial semantic properties of programs are undecidable
  • Rice’s theorem (1951)

Chaitin:

[M]y information-theoretic approach to incompleteness makes incompleteness appear pervasive and natural. This is because algorithmic information theory sometimes enables one to measure the information content of a set of axioms and of a theorem and to deduce that the theorem cannot be obtained from the axioms because it contains too much information.

This suggests to me that sometimes to prove more one must assume more, in other words, that sometimes one must put more in to get more out.⁷⁸

More:

• Gödel was a platonist, a (religious) realist.
• Armstrong, S. (2012). Completeness, incompleteness, and what it all means: first versus second order logic.
• Hilbert’s program is challenged by incompleteness.
• Discuss how incompleteness is overblown in overly epistemically defeatist ways.
  • Seems to indicate that no formal system lacks the full context for everything. Additional axioms will be appropriate for introducing further contexts.
  • Franzén, T. (2005). Gödel’s Theorem: An incomplete guide to its use and abuse.⁷⁹
• Seely, R.A. Gödel on the net.
• Video: Veritasium - Math Has a Fatal Flaw
• Lloyd, S. (1993). Quantum-mechanical computers and uncomputability.⁸⁰
• Cubitt, T., Perez-Garcia, D., & Wolf, M. (2015). Undecidability of the spectral gap.⁸¹

Relationship to mind:

• Lucas-Penrose Argument about Gödel’s Theorem - IEP

See also:

• Artificial intelligence
• Formalism
• Hilbert’s program
• Incompleteness of second-order logic

Complexity theory

• Church-Turing thesis
  • Gödel-Church-Turing
  • Ord, T. (2024). Bounds on the rates of growth and convergence of all physical processes.⁸²
• Scott Aaronson’s Complexity Zoo
• Aaronson, S. (2011). Why philosophers should care about computational complexity.⁸³
• Savage, J.E. (2008). Models of Computation: Exploring the Power of Computing.
• Fagin’s theorem

See also:

• Proof theory

Category theory

Introduction

• Category theory - nLab
• Eilenberg, S. & MacLane, S. (1945). General theory of natural equivalences.⁸⁴
• Rodin, A. (2012). Axiomatic method and category theory.⁸⁵
• Spivak, D.I. (2013). Category theory for scientists.⁸⁶
• Fong, B. & Spivak, D.I. (2018). Seven sketches in compositionality: An invitation to applied category theory.⁸⁷
• Bradley, T.D. (2018). What is applied category theory?⁸⁸
• Categorical product
  • Cook, J.D. (2016). Categorical products.
  • Zucker, P. (2020). Computational category theory in python I: Dictionaries for FinSet.
  • Zucker, P. (2020). Computational category theory in python II: numpy for FinVect.
  • Zucker, P. (2020). Computational category theory in python III: Monoids, groups, and preorders.
  • For the category of abelian groups, the coproduct is the direct sum.
• Functors
• Yoneda lemma
  • Related to: Pragmatic maxim, Identity of indiscernibles
• Relation to set theory
• Relation to Russell type theory
• Univalent foundations
  • Lawvere, F.W. (1963). Functorial Semantics of Algebraic Theories and Some Algebraic Problems in the context of Functorial Semantics of Algebraic Theories.⁸⁹
• Categories are semigroupoids.
• Curry-Howard-Lambek correspondence
  • Three-way isomorphism between intuitionistic logic, typed lambda calculus, and cartesian closed categories

See also:

• Univalent foundations

History

• Samuel Eilenberg (1913-1998) and Saunders Mac Lane (1909-2005)
• Alexander Grothendieck (1928-2014)
• Bill Lawvere (b. 1937)

Grothendieck:

If there is one thing in mathematics that fascinates me more than anything else (and doubtless always has), it is neither “number” nor “size,” but always form. And among the thousand-and-one faces whereby form chooses to reveal itself to us, the one that fascinates me more than any other and continues to fascinate me, is the structure hidden in mathematical things.⁹⁰

Homotopy type theory

• Homotopy type theory (HoTT)
• Intuitionistic type theory
  • Per Martin-Löf (b. 1942)
• Homotopy type theory - nLab
• Homotopy Type Theory: Univalent Foundations of Mathematics (2013)

See also:

• Univalent foundations

Cobordism hypothesis

• Cobordism hypothesis - nLab
• Baez, J.C. & Dolan, J. (1995). Higher‐dimensional algebra and topological quantum field theory.⁹¹
• Baez, J.C. & Stay, M. (2009). Physics, topology, logic, and computation: A Rosetta Stone.⁹²
• Lurie, J. (2009). On the classification of topological field theories.
• Jacob Lurie’s Home Page
• Morton, J. (2013). Blog on the cobordism hypothesis.

See also:

• Topological QFT

Topos theory

• Baez, J. (2021). Topos theory in a nutshell.

Applications

• Univalent foundations
• Functional programming
• Language models
  • Bradley, T.D., Terilla, J., & Vlassopoulos, Y. (2021). An enriched category theory of language: from syntax to semantics.⁹³

See also:

• Univalent foundations

Unification programs

Introduction

Yanofsky, N.S. (2016). Why mathematics works so well:

When you have two distinct fields of mathematics and they are shown to be intimately related in a way that results of one field can be used to get results of another field, you have a type of unification. An example of such unification is monstrous moonshine. This subject describes the shocking connection between the monster group and modular functions. Another example is the Langlands program which connects Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups. The Erlangen program can also be seen as a way of unifying different types of geometries using group theory. In all these examples of unifications, there is a function (or an isomorphism) from the domain of discourse of one field to the domain of discourse of another field. The symmetries of one field (the true mathematical statements) will than map to symmetries of the other field. Category theory is an entire branch of mathematics that was created to describe such unifications. The founders of category theory invented a language that was based on algebraic topology, which is a branch of mathematics that unifies algebra and topology. Category theory is now used in many areas to show that seemingly different parts of mathematics (and physics and theoretical computer science) are closely related.⁹⁴

Erlangen program

• Erlangen program
• A program proposed by Felix Klein in 1872 to classify geometries based on their symmetry groups.

Langlands program

• Langlands program
  • Proposed by Robert Langlands (1967, 1970)
• Geometric Langlands correspondence
  • It translates number-theoretic problems into geometric ones.
• Fundamental lemma
  • Proved by Gérard Laumon and Ngô Bảo Châu (2010)
• Endoscopic groups
• Local Langlands correspondence vs global
• Frenkel, E. (2005). Lectures on the Langlands program and conformal field theory.⁹⁵
• Gaitsgory, D., Raskin, S., et al. (2024). Proof of the geometric Langlands conjecture. (May 2024).

Univalent foundations

• Univalent foundations
• Proposed by Vladimir Voevodsky, 2006-2009.
• Category theory
• Introduction to Univalent Foundations of Mathematics with Agda

See also:

• Category theory
• Hilbert’s program

Platonism

Introduction

What has been is what will be,
and what has been done is what will be done;
there is nothing new under the sun.
Is there a thing of which it is said,
“See, this is new?”
It has already been,
in the ages before us.⁹⁶

• Podnieks, K. (1992). Platonism, intuition, and the nature of mathematics.

Pythagoreanism

• Radical realism
• Monism: everything is math.
• Tegmark, M. (2014). Our Mathematical Universe.⁹⁷

Plato

• Realist
• Theory of the forms
• Dualism: the world and forms?
• The Academy (387 BCE - 529 CE): “Let no one ignorant of geometry enter”
• Mathematics is descriptive of a real but trans-empirical realm.
• Plato perhaps doubts Platonism in Parmenides
• Aristotle on universals

I think you know that the students of geometry, calculation, and the like hypothesize the odd and the even, the various figures, the three kinds of angles, and other things akin to these in each of their investigations, as if they knew them. They make their hypotheses and don’t think it necessary to give any account of them, either to themselves or to others, as if they were clear to everyone. And going from these first principles through the remaining steps, they arrive in full agreement.

I certainly know as much.

Then you also know that, although they use visible figures and make claims about them, their thought isn’t directed to them but to those other things that they are like. They make claims for the sake of the square itself and the diagonal itself, not the diagonal they draw, and similarly with the others. These figures that they make and draw, of which shadows and reflections in water are images, they now in turn use as images, in seeking to see those others themselves that one cannot see except by means of thought.⁹⁸

• A very platonist math documentary

Contemporary platonism

• Quine’s “reluctant platonism”
  • Indispensability argument
  • Quine, W.V.O. (1948). On what there is.⁹⁹
  • distinction between meaning and naming

Whatever we say with the help of names can be said in a language which shuns names altogether. To be assumed as an entity is, purely and simply, to be reckoned as the value of a variable. In terms of the categories of traditional grammar, this amounts roughly to saying that to be is to be in the range of reference of a pronoun. Pronouns are the basic media of reference; nouns might better have been named propronouns. The variables of quantification, ‘something,’ ‘nothing,’ ‘everything,’ range over our whole ontology, whatever it may be; and we are convicted of a particular ontological presupposition if, and only if, the alleged presuppositum has to be reckoned among the entities over which our variables range in order to render one of our affirmations true.¹⁰⁰

a theory is committed to those and only those entities to which the bound variables of the theory must be capable of referring in order that the affirmations made in the theory be true.¹⁰¹

• Neopythagoreanism: Tegmark. (2008). “The mathmatical universe.”¹⁰²
  • Mathematical Universe Hypothesis (MUH)
• Seth Lloyd - the universe is a computer - pythagorean?
• Clearly Ed Witten is a platonist. Video: How is mathematics truth and beauty? Closer To Truth.
• De Cruz, H. (2016). Numerical cognition and mathematical realism.¹⁰³
• Carroll, S. (2021). Mindscape 127: Justin Clarke-Doane on Mathematics, Morality, Objectivity, and Reality.
• Abstract object theory
  • Alexius Meinong (1853-1920)
  • Ernst Mally (1879-1944)
  • Edward N. Zalta (b. 1952)
  • The Metaphysics Research Lab - Stanford, CA
  • Zalta, E.N. (1983). Abstract Objects: An Introduction to Axiomatic Metaphysics.¹⁰⁴
  • Zalta, E.N. (2024). Principia Logico-Metaphysica (Draft).¹⁰⁵
• Basic formal ontology
  • Barry Smith (b. 1952)
• John Conway (1937-2020)
  • Surreal numbers

Visual proofs

• Proofs without words

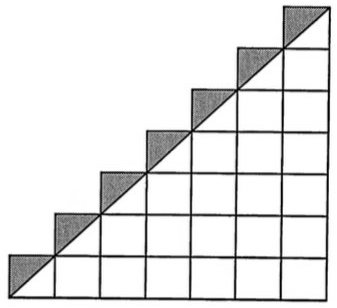
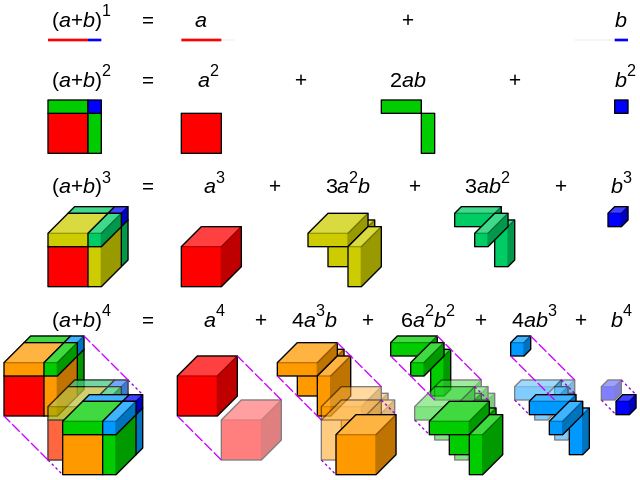
Criticism:

• 3Blue1Brown. (2022). Video: How to lie using visual proofs.

Nominalism

Introduction

• Antirealist

History

Antisthenes:

A horse I can see, but horsehood I cannot see.

• Plato: “Third Man Argument” in Parmenides
• Medieval nominalism
  • Medieval Problem of Universals
  • Roscellinus (c. 1050 - c. 1125)
  • Ockham, William of (1287-1347)
• Modern nominalism

Bayes:

It is not the business of a mathematician to show that a straight line or circle can be drawn, but he tells you what he means by these; and if you understand him, you may proceed further with him; and it would not be to the purpose to object that there is no such thing in nature as a true straight line or perfect circle, for this is none of his concern: he is not inquiring how things are in matter of fact, but supposing things to be in a certain way, what are the consequences to be deduced from them.¹⁰⁶

Johwn Stuart Mill:

Nominalists, who, repudiating Universal Substances, held that there is nothing general except names.¹⁰⁷

• Positivism, Carnap, ESO
• Goodman & Quine¹⁰⁸
• Henkin, L. (1953). Some notes on nominalism.¹⁰⁹
• Azzouni, J. (2015). Nominalism, the nonexistence of mathematical objects.¹¹⁰

See also:

• Natural kinds

Science Without Numbers

Field: Abstract platonic entities, were they to exist, could not interact causally with the world.¹¹¹

• Field: Science Without Numbers¹¹²
• John Burgess¹¹³
• Bueno¹¹⁴
• Chen, E.K. (2018). The intrinsic structure of quantum mechanics.¹¹⁵

significant in context but naming nothing.¹¹⁶

Logicism

Introduction

• A program to derive all or part of mathematics from logic.
• Richard Dedekind (1831-1916)
• Gottlob Frege (1848-1925)
  • All mathematical structures can be constructed from sets and natural numbers.
  • Natural numbers can be constructed from sets.
  • The properties of sets can be reduced to logic. Sets are the extensions of arbitrary conditions.
• Giuseppe Peano (1858-1932)
• Bertrand Russell (1872-1970)
• Alfred North Whitehead (1861-1947)
• Ernst Zermelo (1871-1953)
  • Sets are not simply the extensions of arbitrary conditions. Some conditions have no corresponding set.
• Realist
• Relationship with positivism?
• Russell, B. (1905). On denoting.¹¹⁷
• Russell expresses support for the platonic “universals”¹¹⁸
• Carnap’s logicism
  • Rudolf Carnap (1931) presents the logicist thesis in two parts:¹¹⁹
    1. The concepts of mathematics can be derived from logical concepts through explicit definitions.
    2. The theorems of mathematics can be derived from logical axioms through purely logical deduction.
  • Marschall, B. (2021). Carnap and Beth on the limits of tolerance.¹²⁰
  • Marschall, B. (2022). Carnap’s philosophy of mathematics.¹²¹
• Snapper, E. (1979). The three crises in mathematics: Logicism, intuitionism and formalism.¹²²
• Shapiro, S. (2000). Thinking about Mathematics: The Philosophy of Mathematics.¹²³
• Hume’s principle
• Frege’s theorem

Principia Mathematica

• Principia Mathematica (1910)
• Alfred North Whitehead (1861-1947)
• Bertrand Russell (1872-1970)
• Russell’s Paradox
• “Failure of PM”

ZFC

• ZFC
• ZFC actually does circumvent Russell’s paradox by restricting the comprehension axiom to already existing sets by the use of subset axioms.

Neologicism

• Crispin Wright (b. 1942)
• Bob Hale (1945-2017)
• Linsky, B. & Zalta, E.N. (2006). What is Neologicism?¹²⁴
• Linsky, B. & Zalta, E.N. (1995). Naturalized platonism versus platonized naturalism¹²⁵
• Leitgeb, H., Nodelman, U., & Zalta, E.N. (2024). A defense of logicism.¹²⁶

Linsky & Zalta:

Our knowledge of mathematics is to be explained in terms of the faculty we use to understand language, since that is the only faculty we need to understand object abstraction.¹²⁷

Formalism

Introduction

• Hilbert
• Antirealist?
• Michael Hallett

Hilbert:

We must know. We shall know.

Hilbert:

Mathematics is a presuppositionless science. To found it I do not need God, as does Kronecker, or the assumption of a special faculty of our understanding attuned to the principle of mathematical induction, as does Poincaré, or the primal intuition of Brouwer, or, finally, as do Russell and Whitehead, axioms of infinity, reducibility, or completeness, which in fact are actual, contentual assumptions that cannot be compensated for by consistency proofs.¹²⁸

• Video: Veritasium - You can’t prove everything that’s true

Hilbert’s program

• Hilbert’s program
• Influenced by Principia Mathematica
• Hilbert, D. (1926). On the infinite.¹²⁹
• Gödel derailed the program
• TODO: What do we expect from proof theory now?

Hilbert wanted math to be

• Consistent?
• Decidable
• Complete

See also:

• Incompleteness
• Proof theory

Intuitionism

Introduction

• Antirealist
• Leopold Kronecker’s finitism was a forerunner of intuitionism in foundations of mathematics.
• Kronecker: “God made the integers, all else is the work of man.”
• L.E.J. Brouwer (1881-1966)
  • Brouwer, L.E.J. (1908). Unreliability of the logical principles.¹³⁰
• Constructive mathematics
• Gisin, N. (2020). Indeterminism in physics and intuitionistic mathematics.¹³¹

See also:

• Alternative logics

Linear logic

• Girard, J.Y. (1987). Linear logic.¹³²

Criticism

Hilbert:

Taking the Principle of the Excluded Middle from the mathematician … is the same as … prohibiting the boxer the use of his fists.¹³³

• Tait, W.W. (1983). Against intuitionism: Constructive mathematics is part of classical mathematics.¹³⁴

Fictionalism

• Antirealist
• Stephen Yablo
• Chris Bateman interviews Stephen Yablo

Structuralism

• Realist
• Awodey, S. (2014). Structuralism, invariance, and univalence.¹³⁵

Naturalism

Unreasonable effectiveness

Philosophy is written in that great book which ever lies before our eyes—I mean the Universe—but we cannot understand it if we do not learn the language and grasp the symbols in which it is written. This book is written in the mathematical language, and the symbols are triangles, circles, and other geometrical figures without whose help it is impossible to comprehend a single word of it, without which one wanders in vain through a dark labyrinth.

– Galileo Galilei. (1623). Il Saggiatore (The Assayer).¹³⁶

• Wigner¹³⁷
• Putnam¹³⁸
• Hamming¹³⁹
• Tegmark: MUH
• Zee: Physics uses simple Lie groups, “Nature is kind”¹⁴⁰
• Dan A. Roberts. (2021). Why is AI hard and Physics simple?¹⁴¹
  • See also: No free lunch theorems

Quine-Putnam indispensability thesis

• Quine
• Putnam¹⁴²

Putnam:

[Q]uantification over mathematical entities is indispensable for science…; therefore we should accept such quantification; but this commits us to accepting the existence of the mathematical entities in question.¹⁴³

Mathematical naturalism

• Maddy
• Realist?
• See the outline on Naturalism.

My thoughts

• What would happen if you asked an alien to solve a Rubik’s cube?

Annotated bibliography

Links and encyclopedia articles

References

---

1. Carter (2009).↩︎

2. Hall (2000).↩︎

3. Zee (2016).↩︎

4. McCrimmon (2000).↩︎

5. Baez (2002).↩︎

6. Westbury (2010).↩︎

7. Dwyer (1967).↩︎

8. Burke (1985).↩︎

9. Frankel (1997).↩︎

10. Frè (2013), ch. 2.↩︎

11. Varadarajan (2003).↩︎

12. Tao (2007).↩︎

13. Sussman & Wisdom (2013).↩︎

14. Tu (2017).↩︎

15. Bronstein, Bruna, Cohen, & Velickovic (2021), p. 56–60.↩︎

16. Connes (1985).↩︎

17. Trioni, S. (2020). Cantor’s attic - Omega.↩︎

18. Hilbert (1926), p. 191.↩︎

19. Hunter (1971).↩︎

20. Monk (1976).↩︎

21. Sullivan (2013).↩︎

22. Smith (2020).↩︎

23. Smith (2022).↩︎

24. Carnap (1958).↩︎

25. Teller (1989).↩︎

26. Bonevac (2003).↩︎

27. MacFarlane (2021).↩︎

28. Open Logic Project (2020).↩︎

29. Sheffer (1913).↩︎

30. Post (1921).↩︎

31. Stillwell (2004).↩︎

32. von Fintel (2011).↩︎

33. Ewald (2018).↩︎

34. Gödel (1929).↩︎

35. Henkin (1996).↩︎

36. Awodey & Forssell (2013).↩︎

37. Bès (2002).↩︎

38. Bès & Choffrut (2022).↩︎

39. Enderton (2009).↩︎

40. Henkin (1950).↩︎

41. B. Russell (1908).↩︎

42. Church (1940).↩︎

43. Kleene (1943).↩︎

44. Rossberg (2004).↩︎

45. Kleene (1952).↩︎

46. Shapiro (1991).↩︎

47. G. Russell (2015).↩︎

48. Boolos (1984).↩︎

49. Jerzak (2009).↩︎

50. Bueno (2010).↩︎

51. Sider (2022).↩︎

52. C. I. Lewis (1917).↩︎

53. Carnap (1947).↩︎

54. Kripke (1959).↩︎

55. D. Lewis (1986).↩︎

56. Carroll (1895).↩︎

57. Priest (1998).↩︎

58. Martínez-Ordaz (2021).↩︎

59. Quine (1986).↩︎

60. Viteri & DeDeo (2022).↩︎

61. Hodges (1997), p. vii.↩︎

62. Hunter (1971), p. 6.↩︎

63. Weiss & D’Mello (2015), p. 1.↩︎

64. Weiss & D’Mello (2015).↩︎

65. Button & Walsh (2018).↩︎

66. Makowsky (1995).↩︎

67. Hodges (1985).↩︎

68. Goldfarb (2005).↩︎

69. Gödel (1931).↩︎

70. Gödel (1995).↩︎

71. Edmonds (2020), p. 96 and TODO: Carnap’s diary.↩︎

72. Goldstein (2005).↩︎

73. Raatikainen (2020).↩︎

74. Tarski (1983).↩︎

75. Tarski (1969).↩︎

76. Church (1936).↩︎

77. Turing (1937).↩︎

78. Atiyah, M. et al. (1994), p. 182.↩︎

79. Franzén (2005).↩︎

80. Lloyd (1993).↩︎

81. Cubitt, Perez-Garcia, & Wolf (2015).↩︎

82. Ord (2024).↩︎

83. Aaronson (2011).↩︎

84. Eilenberg & MacLane (1945).↩︎

85. Rodin (2012).↩︎

86. Spivak (2013).↩︎

87. Fong & Spivak (2018).↩︎

88. Bradley (2018).↩︎

89. Lawvere (1963).↩︎

90. TODO↩︎

91. Baez & Dolan (1995).↩︎

92. Baez & Stay (2009).↩︎

93. Bradley, Terilla, & Vlassopoulos (2021).↩︎

94. Yanofsky (2016) In Aguirre, Foster, & Merali (2016), p. 153.↩︎

95. Frenkel (2005).↩︎

96. Ecclesiastes 1:9–10 (NRSV).↩︎

97. Tegmark (2014).↩︎

98. Plato, Republic VI 510c, Cooper & Hutchinson (1997), p. 1131.↩︎

99. Quine (1948).↩︎

100. Quine (1948), p. 7.↩︎

101. Quine (1948), p. 9.↩︎

102. Tegmark (2008).↩︎

103. De Cruz (2016).↩︎

104. Zalta (1983).↩︎

105. Zalta (2024).↩︎

106. Bayes (1736), p. 9–10.↩︎

107. Mill (1877).↩︎

108. Goodman & Quine (1947).↩︎

109. Henkin (1953).↩︎

110. Azzouni (2015).↩︎

111. Field (1989), p. 68. TODO: Get exact quote.↩︎

112. Field (2016).↩︎

113. Burgess (1983).↩︎

114. Bueno (2013).↩︎

115. Chen (2018).↩︎

116. Goodman & Quine (1947), p. 105.↩︎

117. B. Russell (1905).↩︎

118. B. Russell (1912), p. 91–118.↩︎

119. Carnap (1983).↩︎

120. Marschall (2021).↩︎

121. Marschall (2022).↩︎

122. Snapper (1979).↩︎

123. Shapiro (2000).↩︎

124. Linsky & Zalta (2006).↩︎

125. Linsky & Zalta (1995).↩︎

126. Leitgeb, Nodelman, & Zalta (2024).↩︎

127. Linsky & Zalta (2006), p. 43.↩︎

128. Hilbert (1967), p. 479. Discussion by Michael J. O’Donnell:

     Well, the tone sounds like hubris again, but this is actually a relatively modest claim, and largely substantiated by events. Mathematics may arguably be understood as the science of forms, which have an objective quality independent of individual beliefs. What is missing here is the claim that a single formal system may embrace all of mathematics at once, and that we may prove that it contains no error. Notice that Hilbert objects to the “actual, contentual assumptions” of Russell and Whitehead. But, recall that Hilbert claims to treat numerical equations contentually, and even seems to regard that as a virtue. It is not the mere contentual quality of Russell’s and Whitehead’s assumptions that Hilbert objects to, but the fact that each particular assumptions is not verifiable by a single computation or finite observation, and furthermore that there is not even a proof that they are consistent with basic numerical equations. Of course, Hilbert’s proposed system never gets its consistency proof either. Oh well.

     ↩︎

129. Hilbert (1926).↩︎

130. Brouwer (1908).↩︎

131. Gisin (2020).↩︎

132. Girard (1987).↩︎

133. Reid (1996), p. 149.↩︎

134. Tait (1983).↩︎

135. Awodey (2014).↩︎

136. Drake (1957), p.237-8.↩︎

137. Wigner (1960).↩︎

138. Putnam (1975b).↩︎

139. Hamming (1980).↩︎

140. Zee (2016), p. 564.↩︎

141. Roberts (2021).↩︎

142. Putnam (1975a), p. TODO.↩︎

143. Putnam (1971), p. 57.↩︎